Next: Orbital Energies Up: Planetary Motion Previous: Kepler's First Law
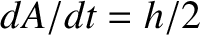 . [See Equation (1.314).]
We have also seen that the planetary orbit is an ellipse. Suppose that
the major and minor radii of the ellipse are
. [See Equation (1.314).]
We have also seen that the planetary orbit is an ellipse. Suppose that
the major and minor radii of the ellipse are 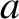 and
and 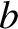 , respectively. It follows that the area of the ellipse is
, respectively. It follows that the area of the ellipse is
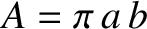 . Now, we expect the
radius vector to sweep out the whole area of the ellipse in a single
orbital period,
. Now, we expect the
radius vector to sweep out the whole area of the ellipse in a single
orbital period,  . Hence,
. Hence,
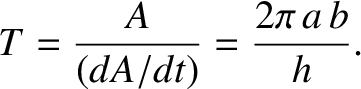 |
(1.322) |
1pt
|
|