According to Equations (1.320) and (1.321), when
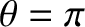 an object moving in the Sun's gravitational
attains its closest distance to the Sun,
an object moving in the Sun's gravitational
attains its closest distance to the Sun,
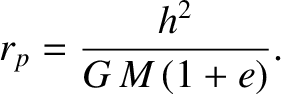 |
(1.324) |
This distance is known as the perihelion distance. At the point of closest approach to the Sun, the
object's instantaneous radial velocity, 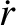 , is zero (because
, is zero (because  attains a minimum value at this point).
Hence, making use of Equations (1.288) and (1.312), the object's speed at the perihelion distance
is
attains a minimum value at this point).
Hence, making use of Equations (1.288) and (1.312), the object's speed at the perihelion distance
is
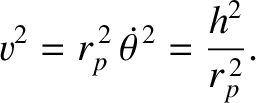 |
(1.325) |
Thus, according to Equation (1.280) and (1.324), the object's energy per unit mass at the perihelion distance is
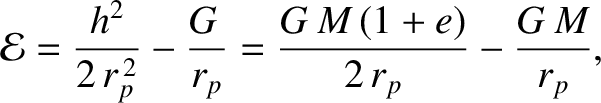 |
(1.326) |
which reduces to
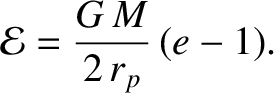 |
(1.327) |
Of course, because  is a conserved quantity, the previous expression specifies the energy per unit
mass of the object at all distances from the Sun. We conclude that an object in an elliptic orbit (
is a conserved quantity, the previous expression specifies the energy per unit
mass of the object at all distances from the Sun. We conclude that an object in an elliptic orbit (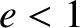 ) has a negative total energy,
whereas an object in a parabolic orbit (
) has a negative total energy,
whereas an object in a parabolic orbit ( ) has zero total energy,
and an object in a hyperbolic orbit (
) has zero total energy,
and an object in a hyperbolic orbit ( ) has a positive total energy. This
makes sense, because in a conservative system in which the potential
energy at infinity is set to zero [see Equation (1.279)], we expect bounded orbits to have negative total energies, and unbounded orbits to have positive
total energies. (See Section 1.3.6.) Thus, elliptical orbits, which are clearly bounded, should indeed have
negative total energies, whereas hyperbolic orbits, which are clearly
unbounded, should indeed have positive total energies. Parabolic orbits
are marginally bounded (i.e., an object executing a parabolic orbit only just escapes from the Sun's gravitational field), and thus have zero total energy.
) has a positive total energy. This
makes sense, because in a conservative system in which the potential
energy at infinity is set to zero [see Equation (1.279)], we expect bounded orbits to have negative total energies, and unbounded orbits to have positive
total energies. (See Section 1.3.6.) Thus, elliptical orbits, which are clearly bounded, should indeed have
negative total energies, whereas hyperbolic orbits, which are clearly
unbounded, should indeed have positive total energies. Parabolic orbits
are marginally bounded (i.e., an object executing a parabolic orbit only just escapes from the Sun's gravitational field), and thus have zero total energy.
 an object moving in the Sun's gravitational
attains its closest distance to the Sun,
This distance is known as the perihelion distance. At the point of closest approach to the Sun, the
object's instantaneous radial velocity,
an object moving in the Sun's gravitational
attains its closest distance to the Sun,
This distance is known as the perihelion distance. At the point of closest approach to the Sun, the
object's instantaneous radial velocity, 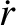 , is zero (because
, is zero (because  attains a minimum value at this point).
Hence, making use of Equations (1.288) and (1.312), the object's speed at the perihelion distance
is
attains a minimum value at this point).
Hence, making use of Equations (1.288) and (1.312), the object's speed at the perihelion distance
is
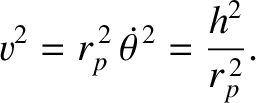
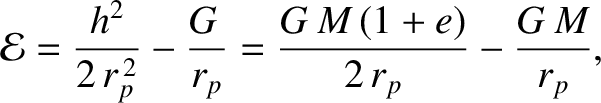
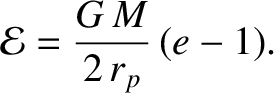
 is a conserved quantity, the previous expression specifies the energy per unit
mass of the object at all distances from the Sun. We conclude that an object in an elliptic orbit (
is a conserved quantity, the previous expression specifies the energy per unit
mass of the object at all distances from the Sun. We conclude that an object in an elliptic orbit (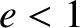 ) has a negative total energy,
whereas an object in a parabolic orbit (
) has a negative total energy,
whereas an object in a parabolic orbit ( ) has zero total energy,
and an object in a hyperbolic orbit (
) has zero total energy,
and an object in a hyperbolic orbit ( ) has a positive total energy. This
makes sense, because in a conservative system in which the potential
energy at infinity is set to zero [see Equation (1.279)], we expect bounded orbits to have negative total energies, and unbounded orbits to have positive
total energies. (See Section 1.3.6.) Thus, elliptical orbits, which are clearly bounded, should indeed have
negative total energies, whereas hyperbolic orbits, which are clearly
unbounded, should indeed have positive total energies. Parabolic orbits
are marginally bounded (i.e., an object executing a parabolic orbit only just escapes from the Sun's gravitational field), and thus have zero total energy.
) has a positive total energy. This
makes sense, because in a conservative system in which the potential
energy at infinity is set to zero [see Equation (1.279)], we expect bounded orbits to have negative total energies, and unbounded orbits to have positive
total energies. (See Section 1.3.6.) Thus, elliptical orbits, which are clearly bounded, should indeed have
negative total energies, whereas hyperbolic orbits, which are clearly
unbounded, should indeed have positive total energies. Parabolic orbits
are marginally bounded (i.e., an object executing a parabolic orbit only just escapes from the Sun's gravitational field), and thus have zero total energy.