Rotational Flattening of Earth
The Earth rotates diurnally with an angular velocity vector,
 , that is directed from the center of
the Earth toward its north geographic pole, and is of magnitude
, that is directed from the center of
the Earth toward its north geographic pole, and is of magnitude
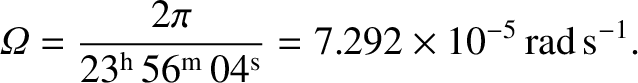 |
(1.351) |
Here,
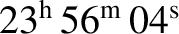 is the length of a so-called sidereal day, and is the
period of the Earth's diurnal rotation relative to the distant stars (as opposed to the Sun).
is the length of a so-called sidereal day, and is the
period of the Earth's diurnal rotation relative to the distant stars (as opposed to the Sun).
Figure 1.19:
Centripetal acceleration.
|
|
Let the Earth's axis of rotation correspond to the  -axis, and let us set up a conventional spherical coordinate system whose
origin is the Earth's center, and whose symmetry axis corresponds to the
-axis, and let us set up a conventional spherical coordinate system whose
origin is the Earth's center, and whose symmetry axis corresponds to the  -axis. (See Section A.23.)
A general point in the Earth whose spherical coordinates are
-axis. (See Section A.23.)
A general point in the Earth whose spherical coordinates are  ,
,  ,
,  rotates at angular velocity
rotates at angular velocity
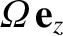 in a circle of radius
in a circle of radius
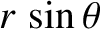 . See Figure 1.19. Thus, according to elementary physics, the point accelerates
toward the
. See Figure 1.19. Thus, according to elementary physics, the point accelerates
toward the  -axis with an acceleration
-axis with an acceleration
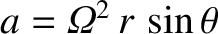 . As is clear from Figure 1.19,
the point's vector acceleration is
. As is clear from Figure 1.19,
the point's vector acceleration is
 |
(1.352) |
where
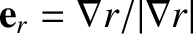 and
and
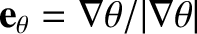 are unit vectors in the spherical
coordinate system.
However, it is easily demonstrated that
are unit vectors in the spherical
coordinate system.
However, it is easily demonstrated that
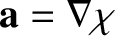 |
(1.353) |
(see Section A.23), where
![$\displaystyle \chi(r,\theta)= -\frac{{\mit\Omega}^2\,r^2}{2}\,\sin^2\theta = \frac{{\mit\Omega}^2\,r^2}{3}\left[P_2(\cos\theta)-1\right]$](img871.png) |
(1.354) |
can be thought of as a kind of centrifugal potential. (Because in the non-inertial frame of reference that co-rotates with the Earth the
point in question would appear to be subject to a fictitious centrifugal force
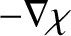 .)
.)
Let us model the interior of the Earth as a fluid of uniform mass density  . [It turns out that the centrifugal potential, (1.354), is sufficiently large that the rigidity of the rock that makes up the Earth is
insufficient to prevent the Earth from responding to the potential in a fluid-like manner.] Now, if
. [It turns out that the centrifugal potential, (1.354), is sufficiently large that the rigidity of the rock that makes up the Earth is
insufficient to prevent the Earth from responding to the potential in a fluid-like manner.] Now, if
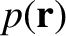 is
the pressure distribution in the interior of the Earth then a small cuboid volume of the Earth lying between
is
the pressure distribution in the interior of the Earth then a small cuboid volume of the Earth lying between  and
and  ,
,  and
and 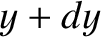 , and
, and  and
and 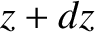 , experiences a net pressure force
, experiences a net pressure force
where
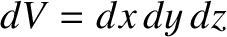 is the volume of the cuboid. (See Section A.19). Thus, the force per unit mass
due to the pressure inside the Earth is
is the volume of the cuboid. (See Section A.19). Thus, the force per unit mass
due to the pressure inside the Earth is
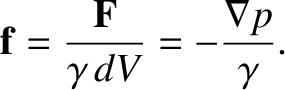 |
(1.356) |
The equation of motion of a general point inside the Earth is
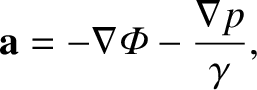 |
(1.357) |
Here, the first term on the right-hand side of the previous equation is the gravitational force per unit mass acting
at the point [see Equation (1.269)], whereas the second term is the force per unit mass due to internal pressure.
Making use of Equation (1.353), we deduce that force balance inside the Earth requires that
 |
(1.358) |
The previous equation can be integrated to give
 |
(1.359) |
where  is a constant.
is a constant.
Let us model the Earth as a spheroid whose outer radius,
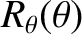 , is specified by Equation (1.328). (See Section 1.10.1.) It follows from Equation (1.350) that the gravitational potential at the
Earth's surface is
, is specified by Equation (1.328). (See Section 1.10.1.) It follows from Equation (1.350) that the gravitational potential at the
Earth's surface is
![$\displaystyle {\mit\Phi}(R_\theta,\theta)\simeq -\frac{G\,M}{R}\left[1+\frac{4}{15}\,\epsilon\,P_2(\cos\theta)\right],$](img888.png) |
(1.360) |
where  is the Earth's mass,
is the Earth's mass,  its mean radius, and
its mean radius, and  its ellipticity.
It is clear from Equation (1.354) that the centrifugal potential at the Earth's surface is
its ellipticity.
It is clear from Equation (1.354) that the centrifugal potential at the Earth's surface is
![$\displaystyle \chi(R_\theta,\theta) \simeq \frac{{\mit\Omega}^2\,R^2}{3}\left[P_2(\cos\theta)-1\right].$](img889.png) |
(1.361) |
Note that we have neglected the slight difference between 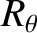 and
and  , when evaluating the previous expression, because the centrifugal potential is
relatively small compared to the gravitational potential [see Equation (1.366)], and
, when evaluating the previous expression, because the centrifugal potential is
relatively small compared to the gravitational potential [see Equation (1.366)], and  is also assumed to be small [see Equation (1.367)]. Now, the
pressure at the Earth's surface must be zero, otherwise the surface would not be in equilibrium with outer space. (Here, we are neglecting the relatively small pressure due to the atmosphere.) It follows from the previous three equations that, on the surface of the Earth,
is also assumed to be small [see Equation (1.367)]. Now, the
pressure at the Earth's surface must be zero, otherwise the surface would not be in equilibrium with outer space. (Here, we are neglecting the relatively small pressure due to the atmosphere.) It follows from the previous three equations that, on the surface of the Earth,
![$\displaystyle -\frac{G\,M}{R}\left[1+\frac{4}{15}\,\epsilon\,P_2(\cos\theta)\right] +\frac{{\mit\Omega}^2\,R^2}{3}\left[P_2(\cos\theta)-1\right] = c.$](img891.png) |
(1.362) |
We can separately equate the components of the previous equation that are independent of  , and
that vary with
, and
that vary with  as
as
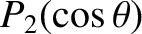 , to give
, to give
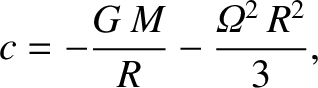 |
(1.363) |
and
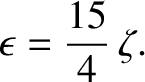 |
(1.364) |
where
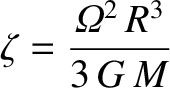 |
(1.365) |
is the ratio of the typical centrifugal acceleration to the typical gravitational acceleration at 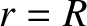 .
.
Given that
 ,
,
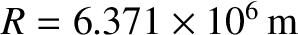 , and
, and
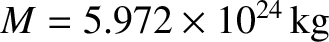 , we deduce that
, we deduce that
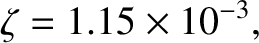 |
(1.366) |
and
 |
(1.367) |
In other words, as consequence of the Earth's rotation, the shape of the Earth is an oblate (because
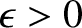 ) spheroid. Thus, the Earth is slightly flattened along an axis passing through its geographic poles. This result was first obtained by Newton. The predicted difference between the Earth's equatorial
and polar radii is
) spheroid. Thus, the Earth is slightly flattened along an axis passing through its geographic poles. This result was first obtained by Newton. The predicted difference between the Earth's equatorial
and polar radii is
 . In fact, the observed ellipticity of the
Earth is
. In fact, the observed ellipticity of the
Earth is
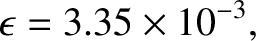 |
(1.368) |
with an associated difference between the equatorial and polar radii of
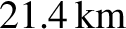 . Our analysis has overestimated the Earth's rotational flattening because, for the sake
of simplicity, we modeled the Earth as a uniform body. In fact, the interior of the Earth is much denser than its
crust.
. Our analysis has overestimated the Earth's rotational flattening because, for the sake
of simplicity, we modeled the Earth as a uniform body. In fact, the interior of the Earth is much denser than its
crust.
 , that is directed from the center of
the Earth toward its north geographic pole, and is of magnitude
Here,
, that is directed from the center of
the Earth toward its north geographic pole, and is of magnitude
Here,
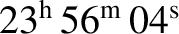 is the length of a so-called sidereal day, and is the
period of the Earth's diurnal rotation relative to the distant stars (as opposed to the Sun).
is the length of a so-called sidereal day, and is the
period of the Earth's diurnal rotation relative to the distant stars (as opposed to the Sun).
 -axis, and let us set up a conventional spherical coordinate system whose
origin is the Earth's center, and whose symmetry axis corresponds to the
-axis, and let us set up a conventional spherical coordinate system whose
origin is the Earth's center, and whose symmetry axis corresponds to the  -axis. (See Section A.23.)
A general point in the Earth whose spherical coordinates are
-axis. (See Section A.23.)
A general point in the Earth whose spherical coordinates are  ,
,  ,
,  rotates at angular velocity
rotates at angular velocity
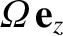 in a circle of radius
in a circle of radius
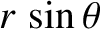 . See Figure 1.19. Thus, according to elementary physics, the point accelerates
toward the
. See Figure 1.19. Thus, according to elementary physics, the point accelerates
toward the  -axis with an acceleration
-axis with an acceleration
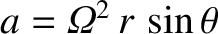 . As is clear from Figure 1.19,
the point's vector acceleration is
. As is clear from Figure 1.19,
the point's vector acceleration is

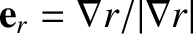 and
and
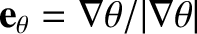 are unit vectors in the spherical
coordinate system.
However, it is easily demonstrated that
(see Section A.23), where
can be thought of as a kind of centrifugal potential. (Because in the non-inertial frame of reference that co-rotates with the Earth the
point in question would appear to be subject to a fictitious centrifugal force
are unit vectors in the spherical
coordinate system.
However, it is easily demonstrated that
(see Section A.23), where
can be thought of as a kind of centrifugal potential. (Because in the non-inertial frame of reference that co-rotates with the Earth the
point in question would appear to be subject to a fictitious centrifugal force
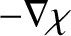 .)
.)
 . [It turns out that the centrifugal potential, (1.354), is sufficiently large that the rigidity of the rock that makes up the Earth is
insufficient to prevent the Earth from responding to the potential in a fluid-like manner.] Now, if
. [It turns out that the centrifugal potential, (1.354), is sufficiently large that the rigidity of the rock that makes up the Earth is
insufficient to prevent the Earth from responding to the potential in a fluid-like manner.] Now, if
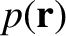 is
the pressure distribution in the interior of the Earth then a small cuboid volume of the Earth lying between
is
the pressure distribution in the interior of the Earth then a small cuboid volume of the Earth lying between  and
and  ,
,  and
and 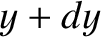 , and
, and  and
and 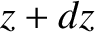 , experiences a net pressure force
, experiences a net pressure force
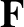
![$\displaystyle = \left[p(x,y,z)-p(x+dx,y,z)\right]dy\,dz\,{\bf e}_x + \left[p(x,y,z)-p(x,y+dy,z)\right]dx\,dz\,{\bf e}_y$](img878.png)
![$\displaystyle \phantom{=}+ \left[p(x,y,z)-p(x,y,z+dz)\right]dx\,dy\,{\bf e}_z$](img879.png)
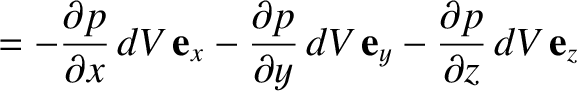
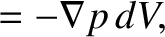
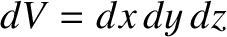 is the volume of the cuboid. (See Section A.19). Thus, the force per unit mass
due to the pressure inside the Earth is
is the volume of the cuboid. (See Section A.19). Thus, the force per unit mass
due to the pressure inside the Earth is
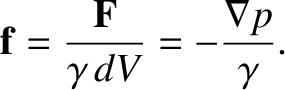
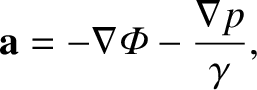


 is a constant.
is a constant.
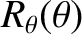 , is specified by Equation (1.328). (See Section 1.10.1.) It follows from Equation (1.350) that the gravitational potential at the
Earth's surface is
, is specified by Equation (1.328). (See Section 1.10.1.) It follows from Equation (1.350) that the gravitational potential at the
Earth's surface is
![$\displaystyle {\mit\Phi}(R_\theta,\theta)\simeq -\frac{G\,M}{R}\left[1+\frac{4}{15}\,\epsilon\,P_2(\cos\theta)\right],$](img888.png)
 is the Earth's mass,
is the Earth's mass,  its mean radius, and
its mean radius, and  its ellipticity.
It is clear from Equation (1.354) that the centrifugal potential at the Earth's surface is
its ellipticity.
It is clear from Equation (1.354) that the centrifugal potential at the Earth's surface is
![$\displaystyle \chi(R_\theta,\theta) \simeq \frac{{\mit\Omega}^2\,R^2}{3}\left[P_2(\cos\theta)-1\right].$](img889.png)
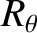 and
and  , when evaluating the previous expression, because the centrifugal potential is
relatively small compared to the gravitational potential [see Equation (1.366)], and
, when evaluating the previous expression, because the centrifugal potential is
relatively small compared to the gravitational potential [see Equation (1.366)], and  is also assumed to be small [see Equation (1.367)]. Now, the
pressure at the Earth's surface must be zero, otherwise the surface would not be in equilibrium with outer space. (Here, we are neglecting the relatively small pressure due to the atmosphere.) It follows from the previous three equations that, on the surface of the Earth,
is also assumed to be small [see Equation (1.367)]. Now, the
pressure at the Earth's surface must be zero, otherwise the surface would not be in equilibrium with outer space. (Here, we are neglecting the relatively small pressure due to the atmosphere.) It follows from the previous three equations that, on the surface of the Earth,
![$\displaystyle -\frac{G\,M}{R}\left[1+\frac{4}{15}\,\epsilon\,P_2(\cos\theta)\right] +\frac{{\mit\Omega}^2\,R^2}{3}\left[P_2(\cos\theta)-1\right] = c.$](img891.png)
 , and
that vary with
, and
that vary with  as
as
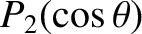 , to give
, to give
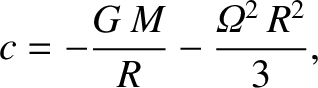
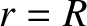 .
.
 ,
,
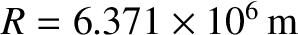 , and
, and
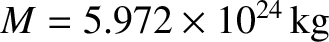 , we deduce that
, we deduce that
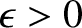 ) spheroid. Thus, the Earth is slightly flattened along an axis passing through its geographic poles. This result was first obtained by Newton. The predicted difference between the Earth's equatorial
and polar radii is
) spheroid. Thus, the Earth is slightly flattened along an axis passing through its geographic poles. This result was first obtained by Newton. The predicted difference between the Earth's equatorial
and polar radii is
 . In fact, the observed ellipticity of the
Earth is
. In fact, the observed ellipticity of the
Earth is
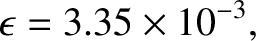
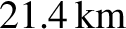 . Our analysis has overestimated the Earth's rotational flattening because, for the sake
of simplicity, we modeled the Earth as a uniform body. In fact, the interior of the Earth is much denser than its
crust.
. Our analysis has overestimated the Earth's rotational flattening because, for the sake
of simplicity, we modeled the Earth as a uniform body. In fact, the interior of the Earth is much denser than its
crust.