Next: Planetary Motion Up: Newtonian Gravity Previous: Gravitational Potential Energy
 situatated in a gravitational field can be
written
where
situatated in a gravitational field can be
written
where  is the object's gravitational potential energy. It is clear from Equation (1.264)
that
is the object's gravitational potential energy. It is clear from Equation (1.264)
that
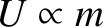 . It follows that the gravitational acceleration of the object,
. It follows that the gravitational acceleration of the object,
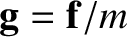 , can
be written
where
, can
be written
where
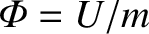 is independent of
is independent of  . The quantity
. The quantity
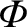 is known as gravitational potential.
is known as gravitational potential.
From Equation (1.264), the gravitational potential due to a point object (or a spherically symmetric object) of mass  situated at the origin
is
situated at the origin
is
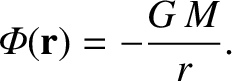 |
(1.270) |
 point objects. Let the
point objects. Let the  th object have mass
th object have mass 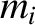 and displacement
and displacement  . Given that
gravity is a superposable force, the generalization of the previous equation is clearly
. Given that
gravity is a superposable force, the generalization of the previous equation is clearly
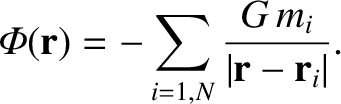 |
(1.271) |
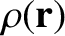 , then the previous expression generalizes to give
where the integral is over all space.
, then the previous expression generalizes to give
where the integral is over all space.
Equation (1.269) can be combined with the differential form of Gauss's theorem, (1.249), to give
Here,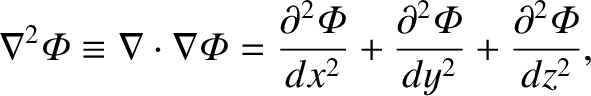 |
(1.274) |
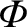 .
(See Section A.21.) Equation (1.273), which specifies the gravitational potential,
.
(See Section A.21.) Equation (1.273), which specifies the gravitational potential,
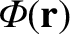 , generated by a
continuous mass distribution of mass density
, generated by a
continuous mass distribution of mass density
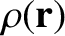 , is known as Poisson's equation. Of course,
Equation (1.272) is the integral form of Poisson's equation.
, is known as Poisson's equation. Of course,
Equation (1.272) is the integral form of Poisson's equation.