Gravitational Potential Energy
Suppose that a spherically symmetric object of mass  is located at the origin of our coordinate system. The
gravitational force, due to the gravitational attraction of mass
is located at the origin of our coordinate system. The
gravitational force, due to the gravitational attraction of mass  , experienced by a point object of mass
, experienced by a point object of mass  and displacement is
and displacement is  (located outside the former mass) is
(located outside the former mass) is
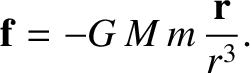 |
(1.257) |
[See Equation (1.241).]
Now,
 . It is easily demonstrated that
Consider
. It is easily demonstrated that
Consider
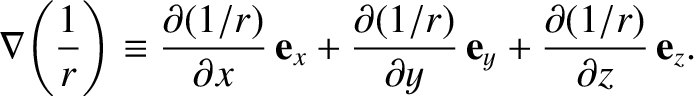 |
(1.261) |
(See Section A.19.)
It follows that
where use has been made of Equations (1.258)–(1.260). The previous equation can
be combined with Equation (1.257) to give
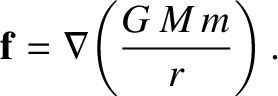 |
(1.263) |
A comparison with Equation (1.47) reveals that the gravitational force field of our spherical object is a conservative field with the associated potential
energy
 |
(1.264) |
Note that, by convention, the potential energy at infinity is zero.
A particle of mass  moving in the gravitational field of our spherical object has a conserved energy
moving in the gravitational field of our spherical object has a conserved energy
 |
(1.265) |
where  is the particle's instantaneous speed. (See Sections 1.3.2 and 1.3.5.)
is the particle's instantaneous speed. (See Sections 1.3.2 and 1.3.5.)
Let us again model the Earth as a sphere of mass  and radius
and radius  that is centered at the origin.
Consider an object that is launched from the surface of the Earth, in an arbitrary outward direction, with
speed
that is centered at the origin.
Consider an object that is launched from the surface of the Earth, in an arbitrary outward direction, with
speed
 . Suppose that the object only just manages to escape from the Earth's gravitational field.
It follows that the object's speed at infinity (i.e.,
. Suppose that the object only just manages to escape from the Earth's gravitational field.
It follows that the object's speed at infinity (i.e., 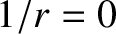 ) is zero. Thus, it is clear from the previous equation that
the object's conserved energy,
) is zero. Thus, it is clear from the previous equation that
the object's conserved energy,  , is also zero. Hence,
, is also zero. Hence,
 |
(1.266) |
at the surface of the Earth,
which implies that
![$\displaystyle v_{\rm escape} = \left(\frac{2\,G\,M}{R}\right)^{1/2}= \left[\fra...
....972\times 10^{24})}{6.371 \times 10^{6}}\right]^{1/2}=11.19\,{\rm km\,s^{-1}}.$](img683.png) |
(1.267) |
The speed
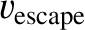 , which is known as the escape speed, is the minimum speed at which an object must be launched
from the Earth's surface if it is to reach outer space.
, which is known as the escape speed, is the minimum speed at which an object must be launched
from the Earth's surface if it is to reach outer space.
 is located at the origin of our coordinate system. The
gravitational force, due to the gravitational attraction of mass
is located at the origin of our coordinate system. The
gravitational force, due to the gravitational attraction of mass  , experienced by a point object of mass
, experienced by a point object of mass  and displacement is
and displacement is  (located outside the former mass) is
[See Equation (1.241).]
Now,
(located outside the former mass) is
[See Equation (1.241).]
Now,
 . It is easily demonstrated that
Consider
. It is easily demonstrated that
Consider
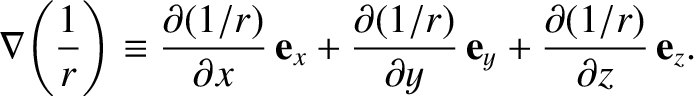
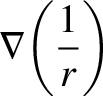
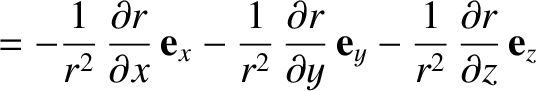

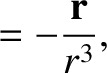
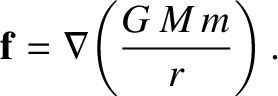
 moving in the gravitational field of our spherical object has a conserved energy
moving in the gravitational field of our spherical object has a conserved energy

 is the particle's instantaneous speed. (See Sections 1.3.2 and 1.3.5.)
is the particle's instantaneous speed. (See Sections 1.3.2 and 1.3.5.)
 and radius
and radius  that is centered at the origin.
Consider an object that is launched from the surface of the Earth, in an arbitrary outward direction, with
speed
that is centered at the origin.
Consider an object that is launched from the surface of the Earth, in an arbitrary outward direction, with
speed
 . Suppose that the object only just manages to escape from the Earth's gravitational field.
It follows that the object's speed at infinity (i.e.,
. Suppose that the object only just manages to escape from the Earth's gravitational field.
It follows that the object's speed at infinity (i.e., 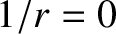 ) is zero. Thus, it is clear from the previous equation that
the object's conserved energy,
) is zero. Thus, it is clear from the previous equation that
the object's conserved energy,  , is also zero. Hence,
, is also zero. Hence,

![$\displaystyle v_{\rm escape} = \left(\frac{2\,G\,M}{R}\right)^{1/2}= \left[\fra...
....972\times 10^{24})}{6.371 \times 10^{6}}\right]^{1/2}=11.19\,{\rm km\,s^{-1}}.$](img683.png)
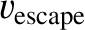 , which is known as the escape speed, is the minimum speed at which an object must be launched
from the Earth's surface if it is to reach outer space.
, which is known as the escape speed, is the minimum speed at which an object must be launched
from the Earth's surface if it is to reach outer space.