Energy Conservation
Consider a particle moving in a conservative force field. Suppose that the particle moves from
point  to point
to point  along some particular path. According to Equation (1.35),
along some particular path. According to Equation (1.35),
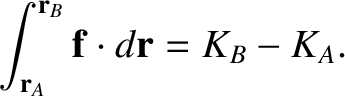 |
(1.48) |
However, Equation (1.41) implies that
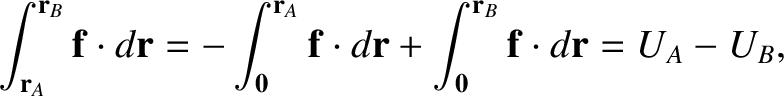 |
(1.49) |
where  is the potential energy at point
is the potential energy at point  , et cetera. The previous two
equations yield
, et cetera. The previous two
equations yield
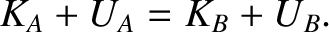 |
(1.50) |
Thus, if we define the total energy,  , of the particle as the sum of its kinetic and potential
energies,
, of the particle as the sum of its kinetic and potential
energies,
 |
(1.51) |
then we deduce that  is a constant of the motion. In other words, the total energy of a particle
moving in a conservative force field is a conserved quantity.
is a constant of the motion. In other words, the total energy of a particle
moving in a conservative force field is a conserved quantity.
 to point
to point  along some particular path. According to Equation (1.35),
along some particular path. According to Equation (1.35),
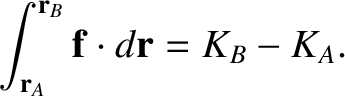
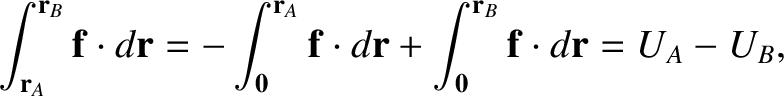
 is the potential energy at point
is the potential energy at point  , et cetera. The previous two
equations yield
, et cetera. The previous two
equations yield
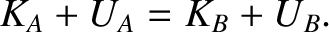
 , of the particle as the sum of its kinetic and potential
energies,
then we deduce that
, of the particle as the sum of its kinetic and potential
energies,
then we deduce that  is a constant of the motion. In other words, the total energy of a particle
moving in a conservative force field is a conserved quantity.
is a constant of the motion. In other words, the total energy of a particle
moving in a conservative force field is a conserved quantity.