Consider a particle subject to a conservative force. Let  be the origin of our coordinate system (i.e., the point whose displacement is
be the origin of our coordinate system (i.e., the point whose displacement is 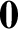 ), and let
), and let  be a general point whose displacement is
be a general point whose displacement is  . We can define the function
. We can define the function
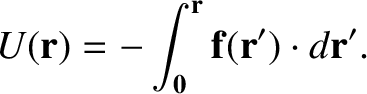 |
(1.41) |
The fact that the force is conservative ensures that this function has a unique value at each point in space.
On the other hand, if the force were non-conservative then the function would be ill-defined, because there are
an infinite number of different paths linking points  and
and  , and each path would yield a different value of the integral on the right-hand side of the previous equation. The quantity
, and each path would yield a different value of the integral on the right-hand side of the previous equation. The quantity  is known as potential energy, and is
the energy that the particle possesses by virtue of its position. Obviously, it only makes sense to associate
potential energy with a conservative force. Note that the fact that the position of the origin of our coordinate system
is arbitrary implies that potential energy is undefined to an arbitrary additive constant. In other words, only
differences in potential energies are physically meaningful.
is known as potential energy, and is
the energy that the particle possesses by virtue of its position. Obviously, it only makes sense to associate
potential energy with a conservative force. Note that the fact that the position of the origin of our coordinate system
is arbitrary implies that potential energy is undefined to an arbitrary additive constant. In other words, only
differences in potential energies are physically meaningful.
Suppose that the particle moves from point  to point
to point
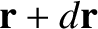 . The associated change in the particle's
potential energy is
. The associated change in the particle's
potential energy is
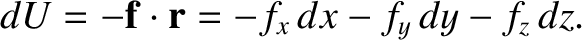 |
(1.42) |
Suppose that 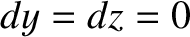 . We can write
. We can write
 |
(1.43) |
Similar arguments yield
Hence, we deduce that
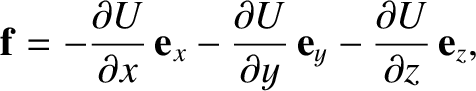 |
(1.46) |
where  is a unit vector parallel to the
is a unit vector parallel to the  -axis, et cetera. (See Section A.4.) The previous equation can
be written more succinctly as
-axis, et cetera. (See Section A.4.) The previous equation can
be written more succinctly as
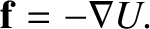 |
(1.47) |
(See Section A.19.)
In other words, a particle moving in a conservative force field experiences a force that is equal to minus the
gradient of the potential energy.
 be the origin of our coordinate system (i.e., the point whose displacement is
be the origin of our coordinate system (i.e., the point whose displacement is 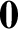 ), and let
), and let  be a general point whose displacement is
be a general point whose displacement is  . We can define the function
The fact that the force is conservative ensures that this function has a unique value at each point in space.
On the other hand, if the force were non-conservative then the function would be ill-defined, because there are
an infinite number of different paths linking points
. We can define the function
The fact that the force is conservative ensures that this function has a unique value at each point in space.
On the other hand, if the force were non-conservative then the function would be ill-defined, because there are
an infinite number of different paths linking points  and
and  , and each path would yield a different value of the integral on the right-hand side of the previous equation. The quantity
, and each path would yield a different value of the integral on the right-hand side of the previous equation. The quantity  is known as potential energy, and is
the energy that the particle possesses by virtue of its position. Obviously, it only makes sense to associate
potential energy with a conservative force. Note that the fact that the position of the origin of our coordinate system
is arbitrary implies that potential energy is undefined to an arbitrary additive constant. In other words, only
differences in potential energies are physically meaningful.
is known as potential energy, and is
the energy that the particle possesses by virtue of its position. Obviously, it only makes sense to associate
potential energy with a conservative force. Note that the fact that the position of the origin of our coordinate system
is arbitrary implies that potential energy is undefined to an arbitrary additive constant. In other words, only
differences in potential energies are physically meaningful.
 to point
to point
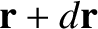 . The associated change in the particle's
potential energy is
. The associated change in the particle's
potential energy is
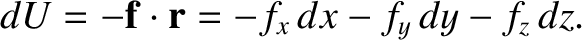
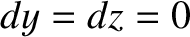 . We can write
. We can write

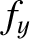
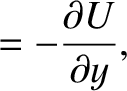
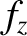
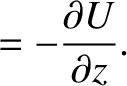
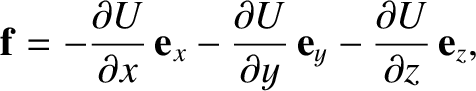
 is a unit vector parallel to the
is a unit vector parallel to the  -axis, et cetera. (See Section A.4.) The previous equation can
be written more succinctly as
(See Section A.19.)
In other words, a particle moving in a conservative force field experiences a force that is equal to minus the
gradient of the potential energy.
-axis, et cetera. (See Section A.4.) The previous equation can
be written more succinctly as
(See Section A.19.)
In other words, a particle moving in a conservative force field experiences a force that is equal to minus the
gradient of the potential energy.