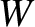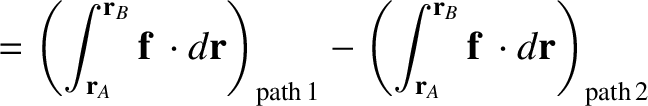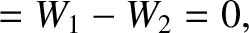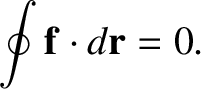Conservative Forces
Suppose, again, that a particle is acted upon by a force
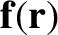 that is a function of the particle's displacement,
that is a function of the particle's displacement,  .
Suppose that the body travels from point
.
Suppose that the body travels from point  to point
to point  along some particular path, labelled
along some particular path, labelled  . The net work done on the
particle is
. The net work done on the
particle is
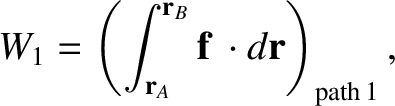 |
(1.36) |
where 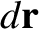 is an element of the path. (See Section A.14.) Suppose, now, that the particle travels between the same two
points along a different path, labelled
is an element of the path. (See Section A.14.) Suppose, now, that the particle travels between the same two
points along a different path, labelled 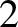 . The net work done on the
particle is
. The net work done on the
particle is
 |
(1.37) |
There are two types of forces in the universe. Conservative forces are such that
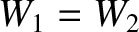 |
(1.38) |
irrespective of the locations of points  and
and  , and the nature of paths
1 and 2. (See Section A.18.) In other words, a conservative force is such that the net work done on a particle moving between
two points is independent of the path taken between the two points. Gravity is an example of a
conservative force. On the other hand, non-conservative forces are such that net work done on a particle moving between
two points depends on the path taken between the two points. Friction is an example of a non-conservative force.
, and the nature of paths
1 and 2. (See Section A.18.) In other words, a conservative force is such that the net work done on a particle moving between
two points is independent of the path taken between the two points. Gravity is an example of a
conservative force. On the other hand, non-conservative forces are such that net work done on a particle moving between
two points depends on the path taken between the two points. Friction is an example of a non-conservative force.
Suppose that the particle is acted on by a conservative force and moves from point  to point
to point  along
path 1, and then from point
along
path 1, and then from point  to point
to point  along path 2. In other words, the particle moves in a closed loop. The net work
done on the particle is
along path 2. In other words, the particle moves in a closed loop. The net work
done on the particle is
where use has been made of the previous three equations. Thus, we conclude that
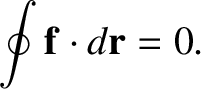 |
(1.40) |
(See Section A.18.)
In other words, if a particle subject to a conservative force moves in a closed loop then zero net work is
done on the particle.
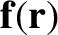 that is a function of the particle's displacement,
that is a function of the particle's displacement,  .
Suppose that the body travels from point
.
Suppose that the body travels from point  to point
to point  along some particular path, labelled
along some particular path, labelled  . The net work done on the
particle is
. The net work done on the
particle is
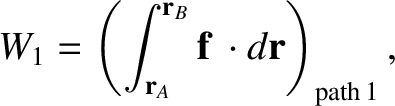
 is an element of the path. (See Section A.14.) Suppose, now, that the particle travels between the same two
points along a different path, labelled
is an element of the path. (See Section A.14.) Suppose, now, that the particle travels between the same two
points along a different path, labelled 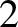 . The net work done on the
particle is
. The net work done on the
particle is

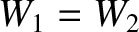
 and
and  , and the nature of paths
1 and 2. (See Section A.18.) In other words, a conservative force is such that the net work done on a particle moving between
two points is independent of the path taken between the two points. Gravity is an example of a
conservative force. On the other hand, non-conservative forces are such that net work done on a particle moving between
two points depends on the path taken between the two points. Friction is an example of a non-conservative force.
, and the nature of paths
1 and 2. (See Section A.18.) In other words, a conservative force is such that the net work done on a particle moving between
two points is independent of the path taken between the two points. Gravity is an example of a
conservative force. On the other hand, non-conservative forces are such that net work done on a particle moving between
two points depends on the path taken between the two points. Friction is an example of a non-conservative force.
 to point
to point  along
path 1, and then from point
along
path 1, and then from point  to point
to point  along path 2. In other words, the particle moves in a closed loop. The net work
done on the particle is
along path 2. In other words, the particle moves in a closed loop. The net work
done on the particle is