Work
Suppose that a particle subject to a force 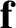 undergoes an infinitesimal displacement
undergoes an infinitesimal displacement 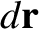 . The
net work that the force does on the particle (i.e., the net energy transferred to the body by the force) is
. The
net work that the force does on the particle (i.e., the net energy transferred to the body by the force) is
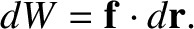 |
(1.28) |
(See Section A.6.)
In other words, the work is the product of the displacement and the component of the force parallel to the
displacement.
It follows from Equation (1.22) that
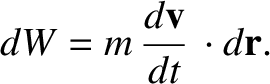 |
(1.29) |
However,
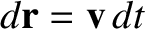 , so we obtain
, so we obtain
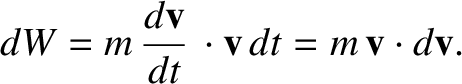 |
(1.30) |
Furthermore,
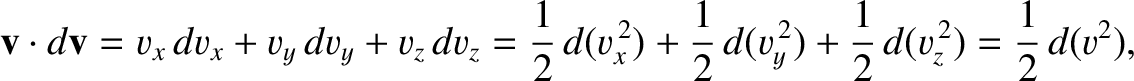 |
(1.31) |
where
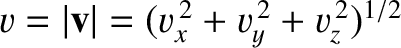 is the particle's speed. It follows from the previous two equations that
is the particle's speed. It follows from the previous two equations that
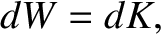 |
(1.32) |
where
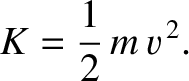 |
(1.33) |
Here, 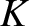 is known as kinetic energy, and is the energy that the particle possesses by virtue of its motion.
Equation (1.32) can be integrated to give the work-energy theorem,
is known as kinetic energy, and is the energy that the particle possesses by virtue of its motion.
Equation (1.32) can be integrated to give the work-energy theorem,
 |
(1.34) |
According to this theorem, the net work done by the force acting on the particle in a given time interval is
equal to the change in the particle's kinetic energy during the same time interval.
Suppose that the force is a function of the particle's displacement,  .
If the particle moves from point
.
If the particle moves from point  to
point
to
point  along any path then Equations (1.28) and (1.34) imply that
along any path then Equations (1.28) and (1.34) imply that
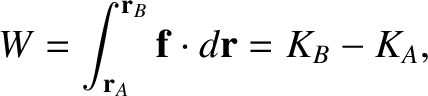 |
(1.35) |
where  denotes the displacement of
point
denotes the displacement of
point  , et cetera,
, et cetera, 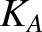 is the kinetic energy at point
is the kinetic energy at point  , et cetera, and
, et cetera, and 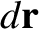 is an element of the path. (See Section A.14.)
is an element of the path. (See Section A.14.)
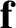 undergoes an infinitesimal displacement
undergoes an infinitesimal displacement 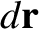 . The
net work that the force does on the particle (i.e., the net energy transferred to the body by the force) is
(See Section A.6.)
In other words, the work is the product of the displacement and the component of the force parallel to the
displacement.
It follows from Equation (1.22) that
. The
net work that the force does on the particle (i.e., the net energy transferred to the body by the force) is
(See Section A.6.)
In other words, the work is the product of the displacement and the component of the force parallel to the
displacement.
It follows from Equation (1.22) that
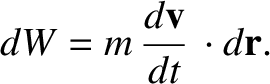
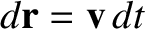 , so we obtain
, so we obtain
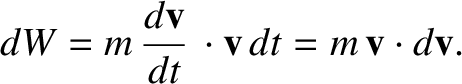
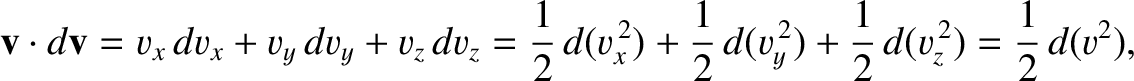
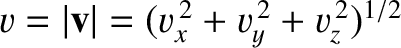 is the particle's speed. It follows from the previous two equations that
where
is the particle's speed. It follows from the previous two equations that
where
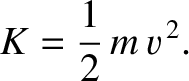
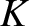 is known as kinetic energy, and is the energy that the particle possesses by virtue of its motion.
Equation (1.32) can be integrated to give the work-energy theorem,
According to this theorem, the net work done by the force acting on the particle in a given time interval is
equal to the change in the particle's kinetic energy during the same time interval.
is known as kinetic energy, and is the energy that the particle possesses by virtue of its motion.
Equation (1.32) can be integrated to give the work-energy theorem,
According to this theorem, the net work done by the force acting on the particle in a given time interval is
equal to the change in the particle's kinetic energy during the same time interval.
 .
If the particle moves from point
.
If the particle moves from point  to
point
to
point  along any path then Equations (1.28) and (1.34) imply that
along any path then Equations (1.28) and (1.34) imply that
 denotes the displacement of
point
denotes the displacement of
point  , et cetera,
, et cetera, 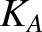 is the kinetic energy at point
is the kinetic energy at point  , et cetera, and
, et cetera, and 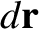 is an element of the path. (See Section A.14.)
is an element of the path. (See Section A.14.)