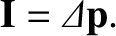Impulse
Consider the motion of a single particle (i.e., a body of negligible spatial extent).
Newton's second law of motion, (1.19), can be written
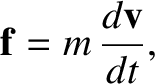 |
(1.22) |
which implies that
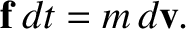 |
(1.23) |
Suppose that the particle in question has an instantaneous velocity 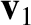 at an initial time
at an initial time 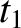 , and an instantaneous velocity
, and an instantaneous velocity
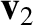 at a final time
at a final time 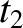 . Integrating the previous equation between the initial and the final time, we
obtain
. Integrating the previous equation between the initial and the final time, we
obtain
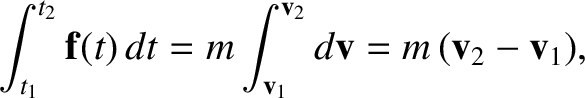 |
(1.24) |
where we have taken into account the fact that the force 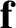 is, in general, a function of time. The quantity
is, in general, a function of time. The quantity
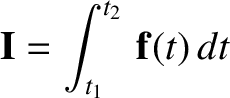 |
(1.25) |
is known as impulse, and is essentially the `area' under the
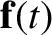 curve between times
curve between times 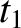 and
and 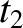 . It is clear from the previous
two equations that
. It is clear from the previous
two equations that
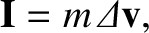 |
(1.26) |
where
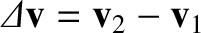 is the change in the particle's velocity between the initial and the final times. Equation (1.18) can be combined with
the previous two equations to give
is the change in the particle's velocity between the initial and the final times. Equation (1.18) can be combined with
the previous two equations to give
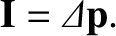 |
(1.27) |
In other words, the net impulse acting on a particle between an initial and a final time is equal to the change in the
momentum of the particle between the same two times.
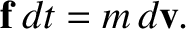
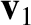 at an initial time
at an initial time 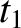 , and an instantaneous velocity
, and an instantaneous velocity
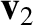 at a final time
at a final time 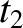 . Integrating the previous equation between the initial and the final time, we
obtain
. Integrating the previous equation between the initial and the final time, we
obtain
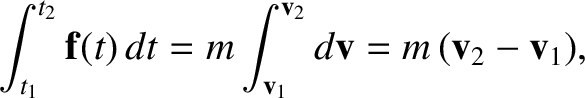
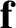 is, in general, a function of time. The quantity
is, in general, a function of time. The quantity
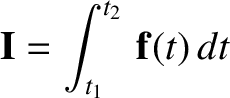
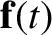 curve between times
curve between times 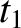 and
and 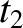 . It is clear from the previous
two equations that
. It is clear from the previous
two equations that
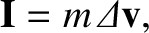
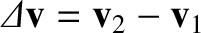 is the change in the particle's velocity between the initial and the final times. Equation (1.18) can be combined with
the previous two equations to give
is the change in the particle's velocity between the initial and the final times. Equation (1.18) can be combined with
the previous two equations to give