Next: Newton's Third Law of Up: Newton's Laws of Motion Previous: Newton's First Law of
The change of motion (i.e., momentum) of a body is proportional to the force impressed upon it, and is made in the direction of the straight line in which the force is impressed.As before, Newton's second law is only valid in an inertial reference frame. Suppose that the body in question has a mass
 , a displacement (from an arbitrary stationary point that forms
the origin of a Cartesian coordinate system that we have set up in our inertial reference frame) r, an instantaneous velocity
, a displacement (from an arbitrary stationary point that forms
the origin of a Cartesian coordinate system that we have set up in our inertial reference frame) r, an instantaneous velocity
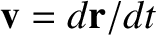 , and
is subject to a force
, and
is subject to a force 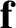 . Here,
. Here,  denotes time. Newton's second law of motion states that
where
is the body's linear momentum.
denotes time. Newton's second law of motion states that
where
is the body's linear momentum.
If the mass of the body is assumed to be constant then Equation (1.17) reduces to
where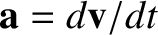 is the body's instantaneous acceleration.
Note that the mass that appears in the previous equation is a measure of the reluctance of the body to
deviate from its preferred state of uniform motion in a straight line due to
the action of a force. This type of mass is known as inertial mass.
However, another type of mass occurs in nature. A body situated in a gravitational field whose local
acceleration is
is the body's instantaneous acceleration.
Note that the mass that appears in the previous equation is a measure of the reluctance of the body to
deviate from its preferred state of uniform motion in a straight line due to
the action of a force. This type of mass is known as inertial mass.
However, another type of mass occurs in nature. A body situated in a gravitational field whose local
acceleration is 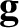 is subject to a gravitational force
is subject to a gravitational force
 |
(1.20) |
Incidentally, the reason that inertial mass is proportional to gravitational mass was not explained until 1916, when Albert Einstein proposed his general theory of relativity. According to this theory, inertial mass is proportional to gravitational mass because it is impossible to distinguish experimentally between a gravitational acceleration and a fictitious acceleration due to motion observed in a non-inertial reference frame. (See Section 1.5.4.)
Acceleration is a vector (i.e., it transforms under rotation of the coordinate axes in an analogous manner to
a displacement), whereas mass is a scalar (i.e., it is invariant under rotation of the coordinate axes). (See Section A.5.) Thus,
it follows from Equation (1.19) that force must be a vector. (Otherwise, the form of Newton's second law would depend unphysically on the arbitrary orientation of the coordinate axes.) One consequence of force being a vector is
that two forces, 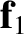 and
and 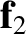 , both acting on a given
body, have the same effect as a single force,
, both acting on a given
body, have the same effect as a single force,
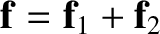 ,
acting on the same body, where the summation is performed according to the
laws of vector addition. (See Section A.3.) Likewise, a single force,
,
acting on the same body, where the summation is performed according to the
laws of vector addition. (See Section A.3.) Likewise, a single force, 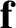 , acting at
on a given body has the same effect as two forces,
, acting at
on a given body has the same effect as two forces, 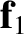 and
and 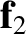 ,
acting on the same body, provided that
,
acting on the same body, provided that
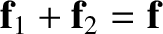 . This
method of combining and splitting forces is known as the resolution of
forces, and lies at the heart of many calculations in classical dynamics.
. This
method of combining and splitting forces is known as the resolution of
forces, and lies at the heart of many calculations in classical dynamics.