Galilean Invariance
Consider a second frame of reference moving with some
arbitrary constant velocity
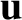 with respect to our original inertial reference frame. We can assume, without loss of generality, that the origins of the
two coordinate systems coincide at time
with respect to our original inertial reference frame. We can assume, without loss of generality, that the origins of the
two coordinate systems coincide at time  . (Note that there is a tacit assumption that clocks run at the same rate in both reference frames. This
is the case provided that the relative speed of the two frames is much smaller than the speed of light in vacuum. See Section 3.2.3.)
It follows that
. (Note that there is a tacit assumption that clocks run at the same rate in both reference frames. This
is the case provided that the relative speed of the two frames is much smaller than the speed of light in vacuum. See Section 3.2.3.)
It follows that
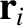 |
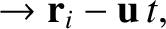 |
(1.98) |
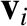 |
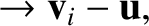 |
(1.99) |
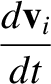 |
 |
(1.100) |
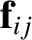 |
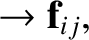 |
(1.101) |
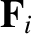 |
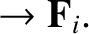 |
(1.102) |
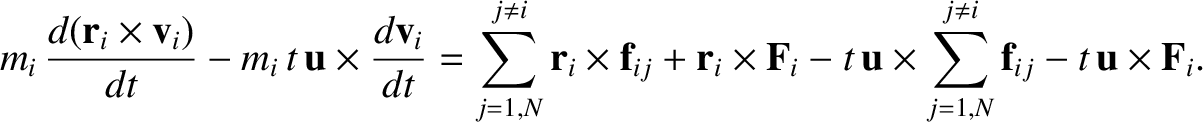 |
(1.103) |
However, the vector product of 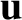 with Equation (1.89) yields
with Equation (1.89) yields
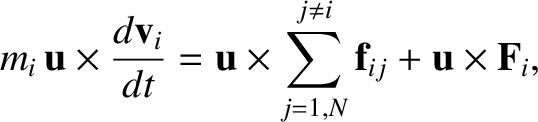 |
(1.104) |
The previous two equations can be combined to give
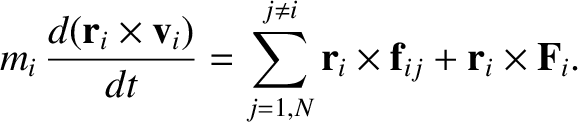 |
(1.105) |
Thus the angular equation of motion, (1.90), also takes the same form in the second reference frame.
It is clear that the second frame of reference is also an inertial reference frame (i.e., a frame in which Newton's
laws of motion are valid). In particular, if all of the forces are zero then the system's constituent particle do not
accelerate in either the first or the second reference frame, in accordance with Newton's first law of motion.
Given that the constant velocity 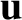 is arbitrary, we conclude that there are an infinite number of different inertial frames of reference all
moving at constant velocities with respect to one another, and that Newton's laws of motion are equally valid in each frame. In particular, if the total energy of the system is conserved in one inertial reference frame then it is
conserved in all inertial reference frames. Likewise, if the total momentum of the system is conserved in one inertial reference frame then it is
conserved in all inertial reference frames. Finally, if the total angular momentum of the system is conserved in one inertial reference frame then it is
conserved in all inertial reference frames.
is arbitrary, we conclude that there are an infinite number of different inertial frames of reference all
moving at constant velocities with respect to one another, and that Newton's laws of motion are equally valid in each frame. In particular, if the total energy of the system is conserved in one inertial reference frame then it is
conserved in all inertial reference frames. Likewise, if the total momentum of the system is conserved in one inertial reference frame then it is
conserved in all inertial reference frames. Finally, if the total angular momentum of the system is conserved in one inertial reference frame then it is
conserved in all inertial reference frames.
Consider the special case in which
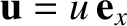 . Let
. Let
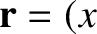 ,
,  ,
, 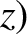 be a general displacement in the
first reference frame, and let
be a general displacement in the
first reference frame, and let
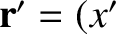 ,
, 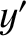 ,
, 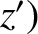 be the corresponding displacement in the second frame.
It follows from Equation (1.98) that
be the corresponding displacement in the second frame.
It follows from Equation (1.98) that
This coordinate transformation was implied in the researches of Galileo Galilei, and is known as a Galilean transformation
in his honor. Hence, the fact that Newton's laws of motion take the same form in all inertial reference frames is
known as Galilean invariance.
Suppose that the second frame of reference accelerates with respect to the first. In other words, suppose that
 . It follows that
. It follows that
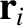 |
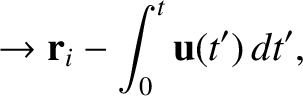 |
(1.109) |
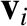 |
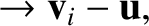 |
(1.110) |
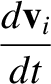 |
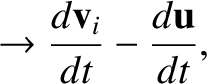 |
(1.111) |
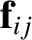 |
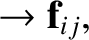 |
(1.112) |
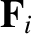 |
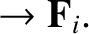 |
(1.113) |
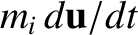 , and the so-called
fictitious torque,
, and the so-called
fictitious torque,
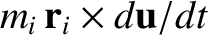 , on the right-hand sides of the previous two
equations. It is clear that the second frame of reference is not an inertial frame. (For instance, if all of the
real forces were zero then the system's constituent particles would still accelerate, which is not in accordance with Newton's
first law of motion.) Hence, we conclude that any frame of reference that accelerates with respect to
a given inertial reference frame is non-inertial.
, on the right-hand sides of the previous two
equations. It is clear that the second frame of reference is not an inertial frame. (For instance, if all of the
real forces were zero then the system's constituent particles would still accelerate, which is not in accordance with Newton's
first law of motion.) Hence, we conclude that any frame of reference that accelerates with respect to
a given inertial reference frame is non-inertial.
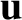 with respect to our original inertial reference frame. We can assume, without loss of generality, that the origins of the
two coordinate systems coincide at time
with respect to our original inertial reference frame. We can assume, without loss of generality, that the origins of the
two coordinate systems coincide at time  . (Note that there is a tacit assumption that clocks run at the same rate in both reference frames. This
is the case provided that the relative speed of the two frames is much smaller than the speed of light in vacuum. See Section 3.2.3.)
It follows that
. (Note that there is a tacit assumption that clocks run at the same rate in both reference frames. This
is the case provided that the relative speed of the two frames is much smaller than the speed of light in vacuum. See Section 3.2.3.)
It follows that
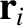
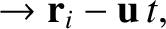
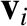
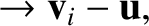
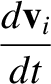

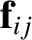
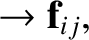
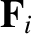
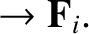
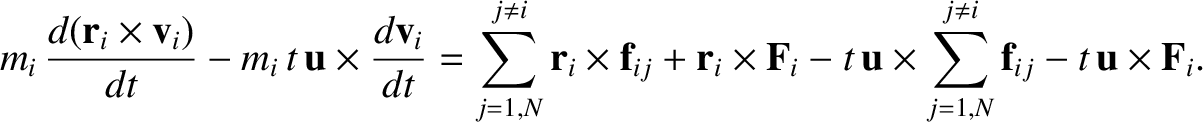
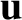 with Equation (1.89) yields
with Equation (1.89) yields
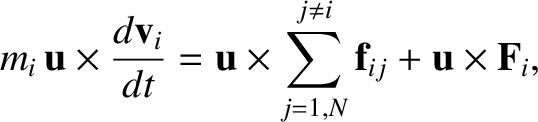
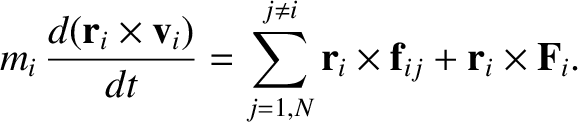
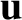 is arbitrary, we conclude that there are an infinite number of different inertial frames of reference all
moving at constant velocities with respect to one another, and that Newton's laws of motion are equally valid in each frame. In particular, if the total energy of the system is conserved in one inertial reference frame then it is
conserved in all inertial reference frames. Likewise, if the total momentum of the system is conserved in one inertial reference frame then it is
conserved in all inertial reference frames. Finally, if the total angular momentum of the system is conserved in one inertial reference frame then it is
conserved in all inertial reference frames.
is arbitrary, we conclude that there are an infinite number of different inertial frames of reference all
moving at constant velocities with respect to one another, and that Newton's laws of motion are equally valid in each frame. In particular, if the total energy of the system is conserved in one inertial reference frame then it is
conserved in all inertial reference frames. Likewise, if the total momentum of the system is conserved in one inertial reference frame then it is
conserved in all inertial reference frames. Finally, if the total angular momentum of the system is conserved in one inertial reference frame then it is
conserved in all inertial reference frames.
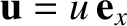 . Let
. Let
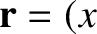 ,
,  ,
, 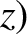 be a general displacement in the
first reference frame, and let
be a general displacement in the
first reference frame, and let
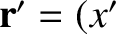 ,
, 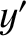 ,
, 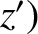 be the corresponding displacement in the second frame.
It follows from Equation (1.98) that
be the corresponding displacement in the second frame.
It follows from Equation (1.98) that
 . It follows that
. It follows that
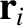
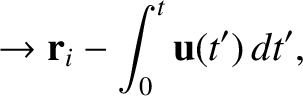
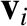
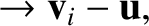
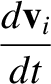
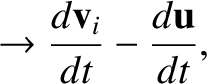
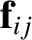
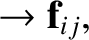
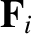
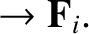
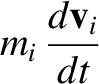
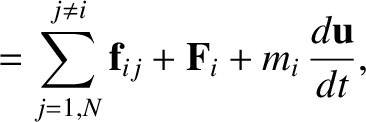
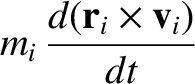
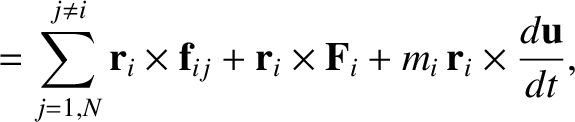
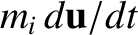 , and the so-called
fictitious torque,
, and the so-called
fictitious torque,
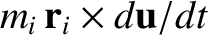 , on the right-hand sides of the previous two
equations. It is clear that the second frame of reference is not an inertial frame. (For instance, if all of the
real forces were zero then the system's constituent particles would still accelerate, which is not in accordance with Newton's
first law of motion.) Hence, we conclude that any frame of reference that accelerates with respect to
a given inertial reference frame is non-inertial.
, on the right-hand sides of the previous two
equations. It is clear that the second frame of reference is not an inertial frame. (For instance, if all of the
real forces were zero then the system's constituent particles would still accelerate, which is not in accordance with Newton's
first law of motion.) Hence, we conclude that any frame of reference that accelerates with respect to
a given inertial reference frame is non-inertial.