Inertial Reference Frame

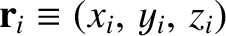Suppose that we have found an inertial frame of reference, and have set up a Cartesian coordinate system in this frame. The motion of particle in the many-particle system discussed in Section 1.4 is specified by giving its displacement, ${\bf r}_i\equiv (x_i,\,y_i,\,z_i)$ , with respect to the origin of the coordinate system, as a function of time, . In particular, the linear and angular equations of motion the particle take the respective forms

$\displaystyle m_i\,\frac{d{\bf v}_i}{dt} = \sum_{j=1,N}^{j\neq i} {\bf f}_{ij} + {\bf F}_i,$

(1.89)

and

$\displaystyle m_i\,\frac{d({\bf r}_i\times {\bf v}_i)}{dt} = \sum_{j=1,N}^{j\neq i} {\bf r}_i\times {\bf f}_{ij} + {\bf r}_i\times {\bf F}_i.$

(1.90)

[See Equations (1.63), (1.79), and (1.81).]