Next: Translational Invariance Up: Invariance Laws Previous: Inertial Reference Frame
 , is, by definition, a vector (i.e., its components,
, is, by definition, a vector (i.e., its components, 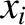 ,
, 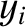 ,
, 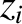 , transform under rotation of the
coordinate axes in such a manner that the length and direction of
, transform under rotation of the
coordinate axes in such a manner that the length and direction of  are preserved).
(See Section A.5.) Moreover,
are preserved).
(See Section A.5.) Moreover, 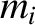 and
and  are scalars (i.e., they are invariant under rotation of the coordinate
axes). It follows that
are scalars (i.e., they are invariant under rotation of the coordinate
axes). It follows that
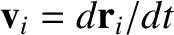 and
and
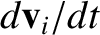 are vectors. Furthermore, we have already
seen that forces are vectors. (See Section 1.2.3.) Finally, we know that if
are vectors. Furthermore, we have already
seen that forces are vectors. (See Section 1.2.3.) Finally, we know that if  and
and 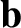 are vectors then
so is
are vectors then
so is
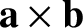 . (See Section A.8.) It follows that every term appearing in the previous two equations
transforms as a vector under rotation of the coordinate axes. In other words, the forms of the linear and angular
equations of motion, (1.89) and (1.90), respectively, are invariant under rotation of the coordinate axes. Of course, this
must be the case because the choice of the orientation of the axes of a Cartesian coordinate system is completely
arbitrary, and has no bearing on the motions of bodies in the universe.
. (See Section A.8.) It follows that every term appearing in the previous two equations
transforms as a vector under rotation of the coordinate axes. In other words, the forms of the linear and angular
equations of motion, (1.89) and (1.90), respectively, are invariant under rotation of the coordinate axes. Of course, this
must be the case because the choice of the orientation of the axes of a Cartesian coordinate system is completely
arbitrary, and has no bearing on the motions of bodies in the universe.