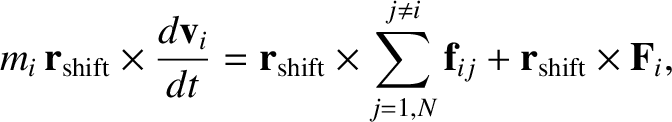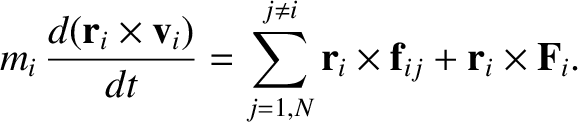Suppose that we transform our coordinate system such that the origin shifts from
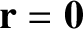 to
to
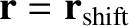 ,
where
,
where
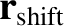 is independent of time.
It follows that
is independent of time.
It follows that
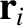 |
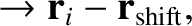 |
(1.91) |
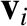 |
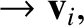 |
(1.92) |
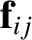 |
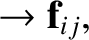 |
(1.93) |
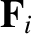 |
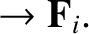 |
(1.94) |
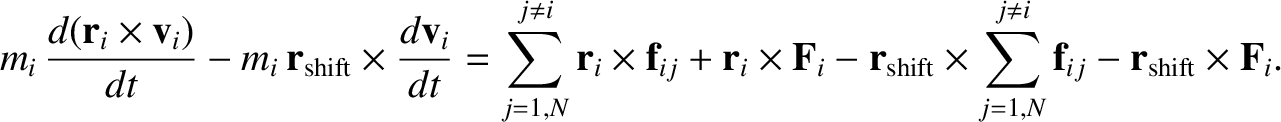 |
(1.95) |
However, the vector product of
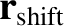 with Equation (1.89) yields
with Equation (1.89) yields
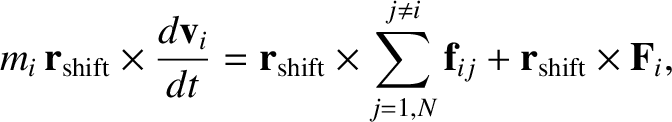 |
(1.96) |
The previous two equations can be combined to give
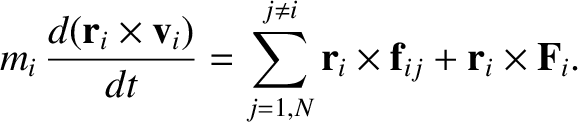 |
(1.97) |
Thus, we conclude that the angular equation of motion, (1.90), is also invariant under the transformation.
Of course, all of this makes sense because the choice of the origin of a Cartesian coordinate system is
completely arbitrary, and has no bearing on the motions of bodies in the universe. One corollary of the previous analysis is that it
does not matter about which point we choose to take moments of momenta and forces to generate angular
momenta and torques, respectively, as long as we choose the same point in all cases.
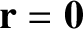 to
to
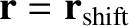 ,
where
,
where
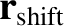 is independent of time.
It follows that
is independent of time.
It follows that
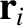
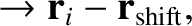
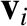
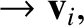
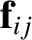
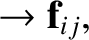
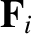
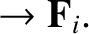
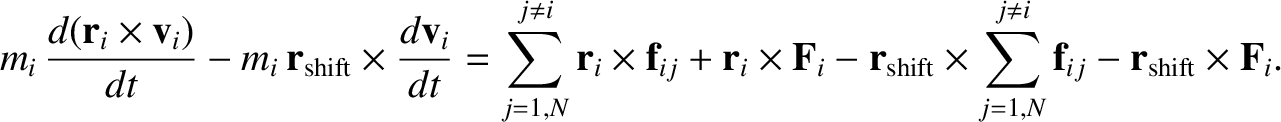
 with Equation (1.89) yields
with Equation (1.89) yields