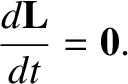Conservation of Angular Momentum
Taking the vector product of Equation (1.63) with the displacement  , we obtain
, we obtain
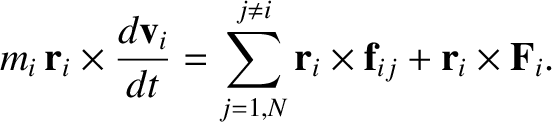 |
(1.78) |
Now, the angular momentum of particle  about the origin of the coordinate system is defined
about the origin of the coordinate system is defined
 |
(1.79) |
(See Section A.8.) It follows that
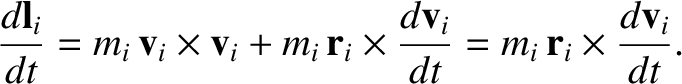 |
(1.80) |
(See Sections A.8 and A.12.) Hence, Equation (1.78) yields the following angular
equation of motion for the  th particle:
th particle:
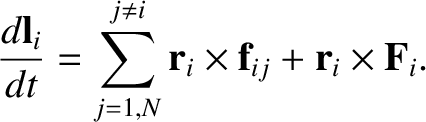 |
(1.81) |
There are  angular equations of motion of analogous form to
the previous equation; one for each particle that makes up the system. We can sum all of
these equations to give
angular equations of motion of analogous form to
the previous equation; one for each particle that makes up the system. We can sum all of
these equations to give
where
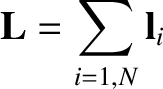 |
(1.83) |
is the total angular momentum of the system about the origin of the coordinate system, and
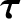 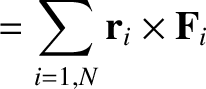 |
(1.84) |
is the net external torque acting on the system about the origin of the coordinate system. (See Section A.8.)
Consider the double sum on the right-hand side of Equation (1.82). A general term,
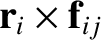 , in this sum can always be paired with a
matching term,
, in this sum can always be paired with a
matching term,
 , in which the indices have been swapped.
Making use of Equation (1.64), the sum of a general matched pair can be written
, in which the indices have been swapped.
Making use of Equation (1.64), the sum of a general matched pair can be written
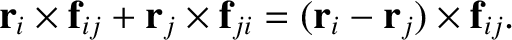 |
(1.85) |
Let us assume that the forces acting between the
various components of the system are central in nature, so
that
 is parallel
to
is parallel
to
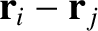 . In other words, the force exerted on particle
. In other words, the force exerted on particle  by particle
by particle  either points directly toward, or directly away from, particle
either points directly toward, or directly away from, particle  ,
and vice versa.
This is a reasonable assumption,
because most of the forces that we encounter in the world around us are of this type (e.g., gravity).
It follows that if the forces are central in nature then the vector product
on the right-hand side of the previous expression is zero. (See Section A.8.)
We conclude that
,
and vice versa.
This is a reasonable assumption,
because most of the forces that we encounter in the world around us are of this type (e.g., gravity).
It follows that if the forces are central in nature then the vector product
on the right-hand side of the previous expression is zero. (See Section A.8.)
We conclude that
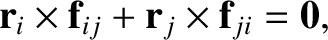 |
(1.86) |
for all values of  and
and  . Thus, the double sum on the right-hand side of Equation (1.82) is zero for any kind of central internal force. We are left with
In particular, if the system is isolated, such that it is not subject to a net external torque, so that
. Thus, the double sum on the right-hand side of Equation (1.82) is zero for any kind of central internal force. We are left with
In particular, if the system is isolated, such that it is not subject to a net external torque, so that
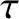
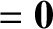 ,
then the previous equation reduces to
,
then the previous equation reduces to
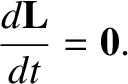 |
(1.88) |
In other words, the total angular momentum of an isolated system is
a conserved quantity, provided that the different components of the
system interact via central forces.
 , we obtain
Now, the angular momentum of particle
, we obtain
Now, the angular momentum of particle  about the origin of the coordinate system is defined
(See Section A.8.) It follows that
about the origin of the coordinate system is defined
(See Section A.8.) It follows that
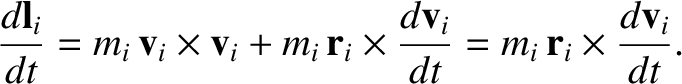
 th particle:
th particle:
 angular equations of motion of analogous form to
the previous equation; one for each particle that makes up the system. We can sum all of
these equations to give
angular equations of motion of analogous form to
the previous equation; one for each particle that makes up the system. We can sum all of
these equations to give
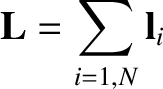
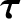
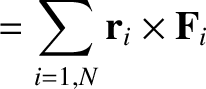
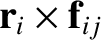 , in this sum can always be paired with a
matching term,
, in this sum can always be paired with a
matching term,
 , in which the indices have been swapped.
Making use of Equation (1.64), the sum of a general matched pair can be written
, in which the indices have been swapped.
Making use of Equation (1.64), the sum of a general matched pair can be written
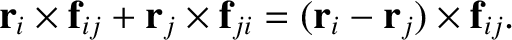
 is parallel
to
is parallel
to
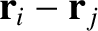 . In other words, the force exerted on particle
. In other words, the force exerted on particle  by particle
by particle  either points directly toward, or directly away from, particle
either points directly toward, or directly away from, particle  ,
and vice versa.
This is a reasonable assumption,
because most of the forces that we encounter in the world around us are of this type (e.g., gravity).
It follows that if the forces are central in nature then the vector product
on the right-hand side of the previous expression is zero. (See Section A.8.)
We conclude that
,
and vice versa.
This is a reasonable assumption,
because most of the forces that we encounter in the world around us are of this type (e.g., gravity).
It follows that if the forces are central in nature then the vector product
on the right-hand side of the previous expression is zero. (See Section A.8.)
We conclude that
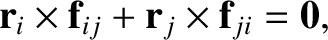
 and
and  . Thus, the double sum on the right-hand side of Equation (1.82) is zero for any kind of central internal force. We are left with
In particular, if the system is isolated, such that it is not subject to a net external torque, so that
. Thus, the double sum on the right-hand side of Equation (1.82) is zero for any kind of central internal force. We are left with
In particular, if the system is isolated, such that it is not subject to a net external torque, so that
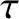
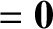 ,
then the previous equation reduces to
,
then the previous equation reduces to