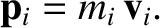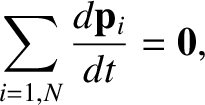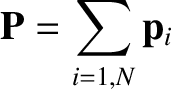Conservation of Linear Momentum
Suppose that our dynamical system is isolated. In other words, the system is not subject to a net external
force, so that
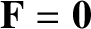 . In this case, Equation (1.66) reduces to
. In this case, Equation (1.66) reduces to
 |
(1.73) |
However, the linear momentum of the  th particle is
th particle is
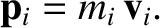 |
(1.74) |
Thus, Equation (1.73) yields
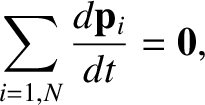 |
(1.75) |
or
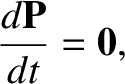 |
(1.76) |
where
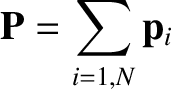 |
(1.77) |
is the total linear momentum of the system. Equation (1.76) implies that the total linear momentum of an isolated
dynamical system is a conserved quantity. In other words, the total momentum does not evolve in time.
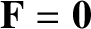 . In this case, Equation (1.66) reduces to
However, the linear momentum of the
. In this case, Equation (1.66) reduces to
However, the linear momentum of the  th particle is
th particle is