Next: Center of Mass Up: Motion of System of Previous: Motion of System of
 particles. Let particle
particles. Let particle  have mass
have mass 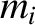 ,
displacement
,
displacement  , and velocity
, and velocity
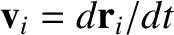 . Suppose that particle
. Suppose that particle  is subject to a force
is subject to a force
 exerted by particle
exerted by particle  .
Suppose, in addition, that particle
.
Suppose, in addition, that particle  is subject to an external force (i.e., a force that originates outside the dynamical
system)
is subject to an external force (i.e., a force that originates outside the dynamical
system)  . Applying Newton's second law of motion to the particle [see Equation (1.19)], we obtain
assuming that all of the forces acting on particle
. Applying Newton's second law of motion to the particle [see Equation (1.19)], we obtain
assuming that all of the forces acting on particle  are superposable. (This is reasonable because
gravitational and electromagnetic forces are superposable.)
Newton's third law of motion, (1.21), can
be generalized to give
for all
are superposable. (This is reasonable because
gravitational and electromagnetic forces are superposable.)
Newton's third law of motion, (1.21), can
be generalized to give
for all  and
and  . Note, in particular, that
. Note, in particular, that
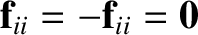 . In other words, particle
. In other words, particle  cannot
exert a force on itself. This accounts for the exclusion of particle
cannot
exert a force on itself. This accounts for the exclusion of particle  in the sum on the right-hand side of Equation (1.63).
in the sum on the right-hand side of Equation (1.63).
There are  equations of motion of analogous form to
Equation (1.63); one for each particle that makes up the system. We can sum all of
these equations to give
equations of motion of analogous form to
Equation (1.63); one for each particle that makes up the system. We can sum all of
these equations to give
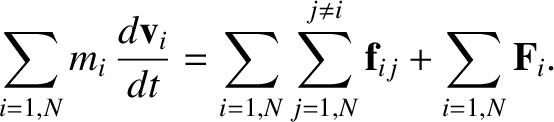 |
(1.65) |
 , appearing in the double sum on the right-hand side of the previous
equation, can be paired with another term—
, appearing in the double sum on the right-hand side of the previous
equation, can be paired with another term—
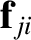 , in this case—that is equal and opposite
according to Newton's third law of motion, (1.64). In other words, the terms in the sum all
cancel out in pairs. It follows that the previous equation reduces to
where
, in this case—that is equal and opposite
according to Newton's third law of motion, (1.64). In other words, the terms in the sum all
cancel out in pairs. It follows that the previous equation reduces to
where
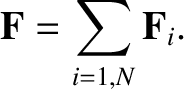 |
(1.67) |