Center of Mass

The center of mass of a dynamical system is an imaginary point whose coordinates are the mass-weighted average of the coordinates of the system's constituent particles. It follows that the displacement of the center of mass is

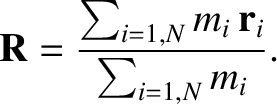$${\bf R} = \frac{\sum_{i=1,N} m_i\,{\bf r}_i}{\sum_{i=1,N} m_i}.$$ (1.68)

The velocity of the center of mass, which is obtained by differentiating the previous expression with respect to time, is

$$\frac{d{\bf R}}{dt} = \frac{1}{M}\sum_{i=1,N} m_i\,{\bf v}_i,$$ (1.69)

where

$$M = \sum_{i=1,N} m_i$$ (1.70)

is the total mass of the system. Likewise, the acceleration of the center of mass is

$$\frac{d^2{\bf R}}{dt^2} = \frac{1}{M}\sum_{i=1,N} m_i\,\frac{d{\bf v}_i}{dt}.$$ (1.71)

A comparison of Equations (1.66) and (1.71) reveals that

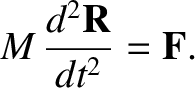$$M\,\frac{d^2{\bf R}}{dt^2} = {\bf F}.$$ (1.72)

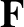We conclude that the center of mass moves like a particle of mass $M$ subject to the net external force, ${\bf F}$, acting on the system. In particular, the motion of the center of mass is completely unaffected by the internal forces that the system's constituent particle exert on one another.