Next: Line Integrals Up: Vector Algebra and Vector Previous: Vector Triple Product
 varies with time, so that
varies with time, so that
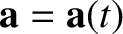 . The time
derivative of the vector is defined
. The time
derivative of the vector is defined
![$\displaystyle \frac{d {\bf a}}{dt} = \lim_{\delta t\rightarrow 0} \left[\frac{{\bf a}(t+\delta t) - {\bf a}(t)}
{\delta t}\right].$](img4681.png) |
(1.63) |
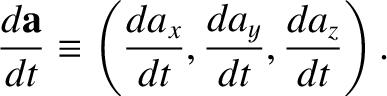 |
(1.64) |
Suppose that  is, in fact, the product of a scalar
is, in fact, the product of a scalar 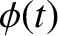 and another vector
and another vector
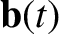 . What now is the time derivative of
. What now is the time derivative of  ? We have
? We have
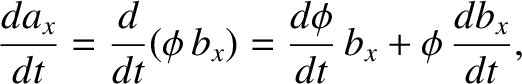 |
(1.65) |
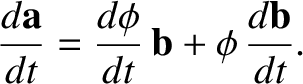 |
(1.66) |
 |
(1.67) |
 |
(1.68) |