Consider a two-dimensional function 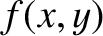 that is defined for all
that is defined for all 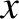 and
and 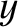 .
What is meant by the integral of
.
What is meant by the integral of 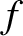 along a given curve joining the points
along a given curve joining the points 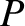 and
and 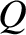 in the
in the 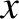 -
-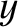 plane?
Well, we first draw out
plane?
Well, we first draw out 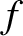 as a function of length
as a function of length 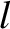 along the path. See Figure A.13. The integral is then simply given
by
along the path. See Figure A.13. The integral is then simply given
by
 |
(1.69) |
where
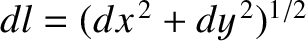 .
.
Figure A.13:
A line integral.
|
|
As an example of this, consider the integral of
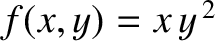 between
between 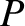 and
and 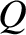 along the
two routes indicated in Figure A.14.
Along route 1 we have
along the
two routes indicated in Figure A.14.
Along route 1 we have 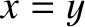 , so
, so
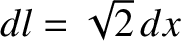 . Thus,
. Thus,
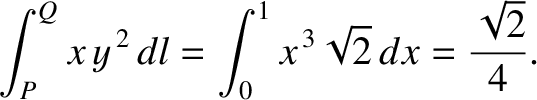 |
(1.70) |
The integration along route 2 gives
Note that the integral depends on the route taken between the initial and final points.
Figure A.14:
An example line integral.
|
|
The most common type of line integral is one in which the contributions from 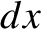 and
and 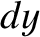 are evaluated
separately, rather that through the path length
are evaluated
separately, rather that through the path length 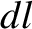 ; that is,
; that is,
![$\displaystyle \int_P^Q \left[ f(x,y)\,dx + g(x,y)\,dy\right].$](img4702.png) |
(1.72) |
As an example of this, consider the integral
![$\displaystyle \int_P^Q \left[ y\,dx + x^{\,3}\,dy\right]$](img4703.png) |
(1.73) |
along the two routes indicated in Figure A.15.
Along route 1 we have 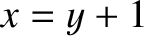 and
and 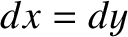 , so
, so
![$\displaystyle \int_P^Q \left[ y\,dx + x^{\,3}\,dy\right]= \int_{0}^1\left[y\,dy + (y+1)^3\,dy\right] = \frac{17}{4}.$](img4706.png) |
(1.74) |
Along route 2,
![$\displaystyle \int_P^Q \left[ y\,dx + x^{\,3}\,dy\right]= \left.\int_0^1 x^{\,3}\,dy\right\vert _{x=1} + \left.\int_1^2 y\,dx\right\vert _{y=1} = \frac{7}{4}.$](img4707.png) |
(1.75) |
Again, the integral depends on the path of integration.
Figure A.15:
An example line integral.
|
|
Suppose that we have a line integral that does not depend on the path of integration. It
follows that
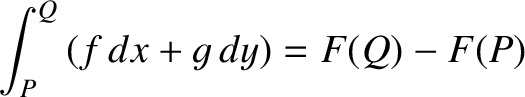 |
(1.76) |
for some function 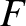 . Given
. Given 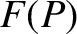 for one point
for one point 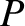 in the
in the 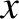 -
-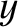 plane, then
plane, then
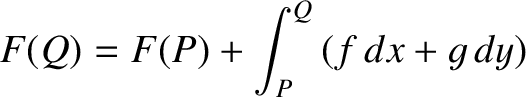 |
(1.77) |
defines 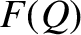 for all other points in the plane. We can then draw a contour map of
for all other points in the plane. We can then draw a contour map of 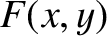 .
The line integral between points
.
The line integral between points 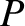 and
and 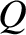 is simply the change in height in the contour
map between these two points:
is simply the change in height in the contour
map between these two points:
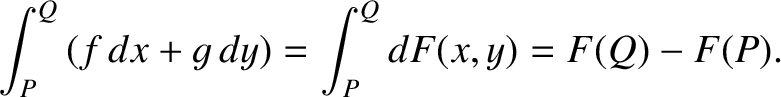 |
(1.78) |
Thus,
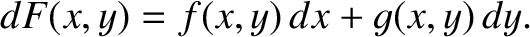 |
(1.79) |
For instance, if
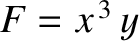 then
then
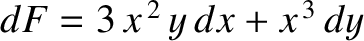 and
and
![$\displaystyle \int_P^Q \left(3\,x^{\,2}\,y\,dx + x^{\,3}\,dy\right) = \left[x^{\,3}\,y\right]_P^Q$](img4718.png) |
(1.80) |
is independent of the path of integration.
It is clear that there are two distinct types of line integral. Those that depend only on their
endpoints and not on the path of integration, and those that depend both on their endpoints
and the integration path. Later on, we shall learn how to distinguish between these two types. (See Section A.18.)
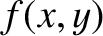 that is defined for all
that is defined for all 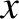 and
and 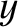 .
What is meant by the integral of
.
What is meant by the integral of 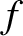 along a given curve joining the points
along a given curve joining the points 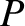 and
and 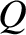 in the
in the 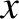 -
-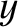 plane?
Well, we first draw out
plane?
Well, we first draw out 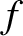 as a function of length
as a function of length 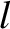 along the path. See Figure A.13. The integral is then simply given
by
along the path. See Figure A.13. The integral is then simply given
by

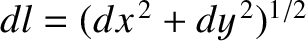 .
.
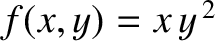 between
between  and
and  along the
two routes indicated in Figure A.14.
Along route 1 we have
along the
two routes indicated in Figure A.14.
Along route 1 we have 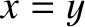 , so
, so
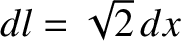 . Thus,
. Thus,
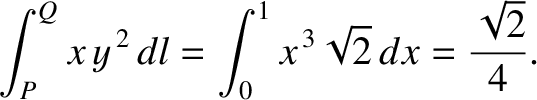
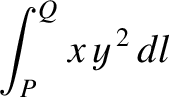
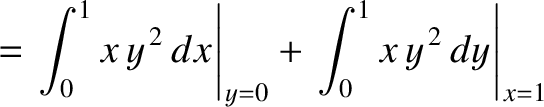
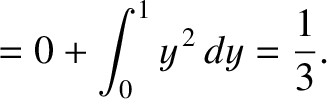
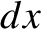 and
and 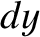 are evaluated
separately, rather that through the path length
are evaluated
separately, rather that through the path length 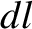 ; that is,
; that is,
![$\displaystyle \int_P^Q \left[ f(x,y)\,dx + g(x,y)\,dy\right].$](img4702.png)
![$\displaystyle \int_P^Q \left[ y\,dx + x^{\,3}\,dy\right]$](img4703.png)
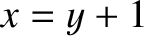 and
and 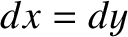 , so
, so
![$\displaystyle \int_P^Q \left[ y\,dx + x^{\,3}\,dy\right]= \int_{0}^1\left[y\,dy + (y+1)^3\,dy\right] = \frac{17}{4}.$](img4706.png)
![$\displaystyle \int_P^Q \left[ y\,dx + x^{\,3}\,dy\right]= \left.\int_0^1 x^{\,3}\,dy\right\vert _{x=1} + \left.\int_1^2 y\,dx\right\vert _{y=1} = \frac{7}{4}.$](img4707.png)
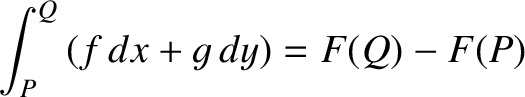
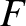 . Given
. Given 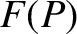 for one point
for one point 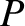 in the
in the 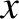 -
-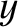 plane, then
plane, then
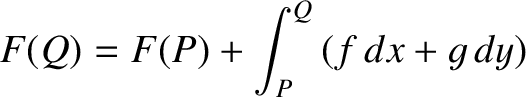
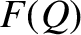 for all other points in the plane. We can then draw a contour map of
for all other points in the plane. We can then draw a contour map of 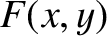 .
The line integral between points
.
The line integral between points 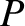 and
and 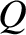 is simply the change in height in the contour
map between these two points:
is simply the change in height in the contour
map between these two points:
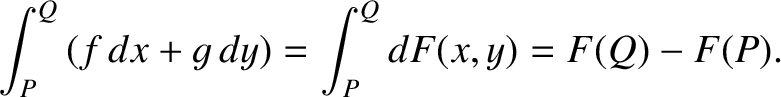
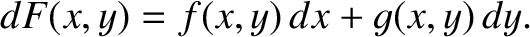
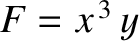 then
then
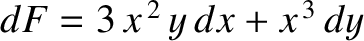 and
and
![$\displaystyle \int_P^Q \left(3\,x^{\,2}\,y\,dx + x^{\,3}\,dy\right) = \left[x^{\,3}\,y\right]_P^Q$](img4718.png)