Next: Length Contraction Up: Theoretical Basis of Special Previous: Invariance of Transverse Lengths
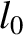 from the clock. Thus, the time taken for the light ray to travel from the clock to the reflector, and back
again,
corresponds to one tick of the clock.
from the clock. Thus, the time taken for the light ray to travel from the clock to the reflector, and back
again,
corresponds to one tick of the clock.
Suppose that we observe the aforementioned clock in a frame of reference that moves with velocity  with respect
to the clock's rest frame, where the direction of
with respect
to the clock's rest frame, where the direction of  is perpendicular to the path of the light ray in the rest frame. See Figure 3.6.
Let
is perpendicular to the path of the light ray in the rest frame. See Figure 3.6.
Let 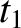 be the time required for a light ray to travel from the clock to the reflector, and back again, in the moving frame.
In the moving frame, the clock moves a parallel (to
be the time required for a light ray to travel from the clock to the reflector, and back again, in the moving frame.
In the moving frame, the clock moves a parallel (to 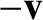 ) distance
) distance  in this time interval.
Note that the transverse distance,
in this time interval.
Note that the transverse distance, 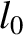 , of the reflector from the clock is the same in both reference frames. (See Section 3.2.2.) It is clear, by symmetry, that in traveling from the clock to the reflector, the light ray in the moving frame
has moved a transverse distance
, of the reflector from the clock is the same in both reference frames. (See Section 3.2.2.) It is clear, by symmetry, that in traveling from the clock to the reflector, the light ray in the moving frame
has moved a transverse distance 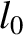 and a parallel (to
and a parallel (to 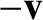 ) distance
) distance  . Moreover, the ray travels the
same transverse and parallel distances in traveling from the reflector back to the clock.
Hence, the net path-length of the light ray is
. Moreover, the ray travels the
same transverse and parallel distances in traveling from the reflector back to the clock.
Hence, the net path-length of the light ray is
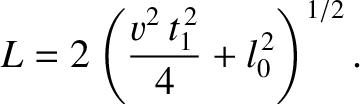 |
(3.67) |
 in the moving frame, according to Einstein's second postulate, we have
in the moving frame, according to Einstein's second postulate, we have
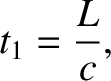 |
(3.68) |
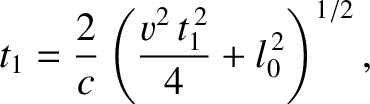 |
(3.69) |
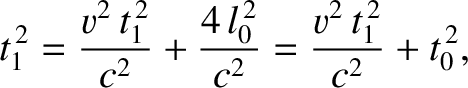 |
(3.70) |
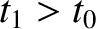 . Given that a tick of our clock corresponds to the time required for a light ray to travel
from the clock to the reflector, and back again, we conclude that the clock ticks more slowly in the
moving reference frame than it does in its rest frame. This effect is known as time dilation.
. Given that a tick of our clock corresponds to the time required for a light ray to travel
from the clock to the reflector, and back again, we conclude that the clock ticks more slowly in the
moving reference frame than it does in its rest frame. This effect is known as time dilation.
We can also conclude that
any type of clock, not just a light-clock, will tick more slowly in a moving reference frame than in its rest frame, by the same factor as our light clock,
otherwise the same experiment (i.e., measuring the time it takes a light ray to travel a distance 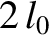 in vacuum using the former type of clock) would
produced different results in different inertial frames, which is forbidden by Einstein's first postulate.
in vacuum using the former type of clock) would
produced different results in different inertial frames, which is forbidden by Einstein's first postulate.
Let us define the so-called Lorentz factor,
Note that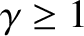 . The time dilation law, (3.71), can be written
In other words, time is dilated by the Lorentz factor in a moving frame of reference.
. The time dilation law, (3.71), can be written
In other words, time is dilated by the Lorentz factor in a moving frame of reference.
Muons are unstable particles that have measured lifetimes of
 in their rest frame.
However, when the Earth's atmosphere is struck by cosmic-ray particles, very energetic muons that move at 98% of the speed of light are produced. The measured lifetimes of these cosmic-ray muons is indeed about five times longer than the rest-frame lifetime of a muon, in accordance with the previous two equations.
in their rest frame.
However, when the Earth's atmosphere is struck by cosmic-ray particles, very energetic muons that move at 98% of the speed of light are produced. The measured lifetimes of these cosmic-ray muons is indeed about five times longer than the rest-frame lifetime of a muon, in accordance with the previous two equations.