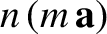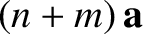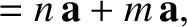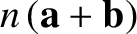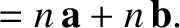Vector Algebra
Figure A.2:
Vector addition.
|
|
Suppose that the displacements
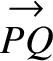 and
and
 represent the vectors
represent the vectors  and
and 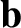 , respectively. See Figure A.2. It can be seen that the result
of combining these two displacements is to give the net displacement
, respectively. See Figure A.2. It can be seen that the result
of combining these two displacements is to give the net displacement
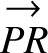 . Hence,
if
. Hence,
if
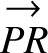 represents the vector
represents the vector  then we can write
then we can write
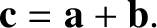 |
(1.1) |
This defines vector addition.
By completing the parallelogram  , we can also see that
, we can also see that
 |
(1.2) |
However,
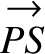 has the same length and direction as
has the same length and direction as
 ,
and, thus, represents the same vector,
,
and, thus, represents the same vector, 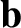 . Likewise,
. Likewise,
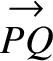 and
and
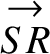 both represent the vector
both represent the vector  . Thus, the previous equation is equivalent to
. Thus, the previous equation is equivalent to
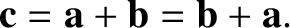 |
(1.3) |
We conclude that the addition of vectors is commutative. It can also
be shown that the associative law holds; that is,
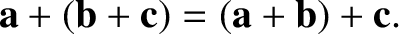 |
(1.4) |
The null vector, 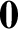 , is represented by a displacement of zero length and arbitrary direction.
Because the result of combining such a displacement with a finite length displacement is the same
as the latter displacement by itself, it follows that
, is represented by a displacement of zero length and arbitrary direction.
Because the result of combining such a displacement with a finite length displacement is the same
as the latter displacement by itself, it follows that
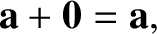 |
(1.5) |
where  is a general vector.
The negative of
is a general vector.
The negative of  is defined as that vector that has the same magnitude, but acts in the opposite direction, and is denoted
is defined as that vector that has the same magnitude, but acts in the opposite direction, and is denoted  .
The sum of
.
The sum of  and
and  is thus
the null vector; in other words,
is thus
the null vector; in other words,
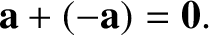 |
(1.6) |
We can also define the difference of two vectors,  and
and 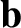 , as
, as
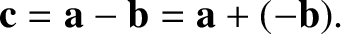 |
(1.7) |
This definition of vector subtraction is illustrated in Figure A.3.
Figure A.3:
Vector subtraction.
|
|
If 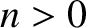 is a scalar then the expression
is a scalar then the expression
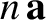 denotes a vector whose direction is the same
as
denotes a vector whose direction is the same
as  , and whose magnitude
is
, and whose magnitude
is  times that of
times that of  . (This definition becomes obvious when
. (This definition becomes obvious when  is an integer.)
If
is an integer.)
If  is negative then, because
is negative then, because
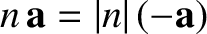 , it follows
that
, it follows
that
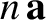 is a vector whose magnitude is
is a vector whose magnitude is 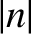 times that of
times that of  , and whose
direction is opposite to
, and whose
direction is opposite to  . These definitions imply that if
. These definitions imply that if  and
and  are
two scalars then
are
two scalars then
 and
and
 represent the vectors
represent the vectors  and
and 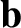 , respectively. See Figure A.2. It can be seen that the result
of combining these two displacements is to give the net displacement
, respectively. See Figure A.2. It can be seen that the result
of combining these two displacements is to give the net displacement
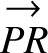 . Hence,
if
. Hence,
if
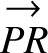 represents the vector
represents the vector 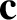 then we can write
then we can write
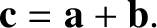
 , we can also see that
, we can also see that

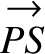 has the same length and direction as
has the same length and direction as
 ,
and, thus, represents the same vector,
,
and, thus, represents the same vector, 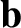 . Likewise,
. Likewise,
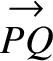 and
and
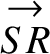 both represent the vector
both represent the vector  . Thus, the previous equation is equivalent to
. Thus, the previous equation is equivalent to
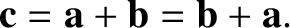
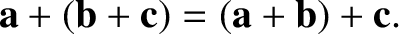
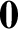 , is represented by a displacement of zero length and arbitrary direction.
Because the result of combining such a displacement with a finite length displacement is the same
as the latter displacement by itself, it follows that
, is represented by a displacement of zero length and arbitrary direction.
Because the result of combining such a displacement with a finite length displacement is the same
as the latter displacement by itself, it follows that
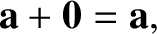
 is a general vector.
The negative of
is a general vector.
The negative of  is defined as that vector that has the same magnitude, but acts in the opposite direction, and is denoted
is defined as that vector that has the same magnitude, but acts in the opposite direction, and is denoted  .
The sum of
.
The sum of  and
and  is thus
the null vector; in other words,
is thus
the null vector; in other words,
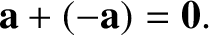
 and
and  , as
, as
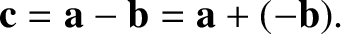
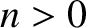 is a scalar then the expression
is a scalar then the expression
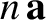 denotes a vector whose direction is the same
as
denotes a vector whose direction is the same
as  , and whose magnitude
is
, and whose magnitude
is  times that of
times that of  . (This definition becomes obvious when
. (This definition becomes obvious when  is an integer.)
If
is an integer.)
If  is negative then, because
is negative then, because
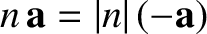 , it follows
that
, it follows
that
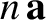 is a vector whose magnitude is
is a vector whose magnitude is 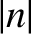 times that of
times that of  , and whose
direction is opposite to
, and whose
direction is opposite to  . These definitions imply that if
. These definitions imply that if  and
and  are
two scalars then
are
two scalars then