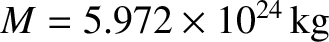Gravitational Field of Earth
Suppose that we model the Earth (not very accurately) as a uniform sphere of mass  and
radius
and
radius  . Let the center of the Earth lie at the origin. We wish to determine the gravitational
acceleration due to the Earth,
. Let the center of the Earth lie at the origin. We wish to determine the gravitational
acceleration due to the Earth, 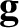 , both inside and outside the Earth. By symmetry, we expect the
gravitational acceleration at a general point whose displacement is
, both inside and outside the Earth. By symmetry, we expect the
gravitational acceleration at a general point whose displacement is  to be directed radially inward toward the center of the Earth, and
to only depend on the radial distance,
to be directed radially inward toward the center of the Earth, and
to only depend on the radial distance,  , from the center of the Earth. In other words,
, from the center of the Earth. In other words,
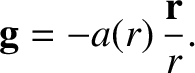 |
(1.250) |
Consider a spherical Gaussian surface,  , of radius
, of radius  , whose center corresponds to the center of the Earth. The flux of gravitational
acceleration out of this surface is
, whose center corresponds to the center of the Earth. The flux of gravitational
acceleration out of this surface is
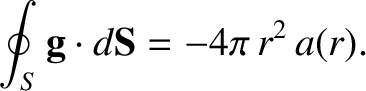 |
(1.251) |
Thus, Gauss's law, (1.246), yields
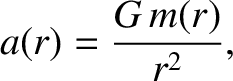 |
(1.252) |
where 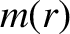 is the mass enclosed by the surface.
Now, if
is the mass enclosed by the surface.
Now, if 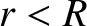 then
then
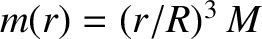 (by proportion), but if
(by proportion), but if 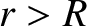 then
then 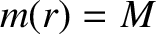 . Thus, we
deduce that
. Thus, we
deduce that
 |
(1.253) |
for 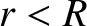 , and
, and
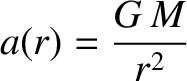 |
(1.254) |
for 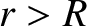 .
In other words, inside the Earth, the gravitational acceleration due to the Earth increases linearly with distance from the
Earth's center, but, outside the Earth, it falls off as the inverse-square of distance from the
Earth's center. In particular, the gravitational field outside the Earth is exactly the
same as that of a point object whose mass is equal to that of the Earth, and that is located at the
Earth's center. This is an example of an important result first derived by Newton; namely, that the
gravitational field outside a spherically symmetric mass distribution is the same as that of a
point object located at the center of the distribution whose mass is equal to that of the distribution.
.
In other words, inside the Earth, the gravitational acceleration due to the Earth increases linearly with distance from the
Earth's center, but, outside the Earth, it falls off as the inverse-square of distance from the
Earth's center. In particular, the gravitational field outside the Earth is exactly the
same as that of a point object whose mass is equal to that of the Earth, and that is located at the
Earth's center. This is an example of an important result first derived by Newton; namely, that the
gravitational field outside a spherically symmetric mass distribution is the same as that of a
point object located at the center of the distribution whose mass is equal to that of the distribution.
It is clear from Equation (1.254) that the gravitational acceleration at the surface of the Earth
is
 |
(1.255) |
Given that the measured (average) gravitational acceleration at the Earth's surface is
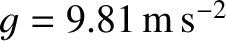 ,
and that the measured (mean) radius of the Earth is
,
and that the measured (mean) radius of the Earth is
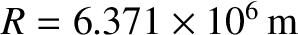 , we arrive at the
following estimate for the Earth's mass,
, we arrive at the
following estimate for the Earth's mass,
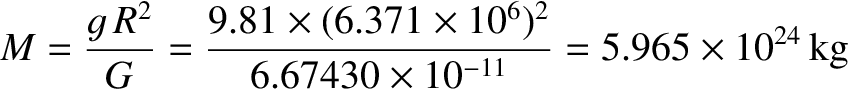 |
(1.256) |
This estimate lies within 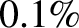 of the correct value, which is
of the correct value, which is
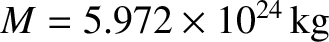
 and
radius
and
radius  . Let the center of the Earth lie at the origin. We wish to determine the gravitational
acceleration due to the Earth,
. Let the center of the Earth lie at the origin. We wish to determine the gravitational
acceleration due to the Earth, 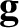 , both inside and outside the Earth. By symmetry, we expect the
gravitational acceleration at a general point whose displacement is
, both inside and outside the Earth. By symmetry, we expect the
gravitational acceleration at a general point whose displacement is  to be directed radially inward toward the center of the Earth, and
to only depend on the radial distance,
to be directed radially inward toward the center of the Earth, and
to only depend on the radial distance,  , from the center of the Earth. In other words,
, from the center of the Earth. In other words,
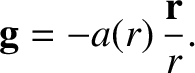
 , of radius
, of radius  , whose center corresponds to the center of the Earth. The flux of gravitational
acceleration out of this surface is
, whose center corresponds to the center of the Earth. The flux of gravitational
acceleration out of this surface is
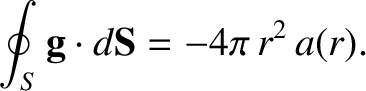
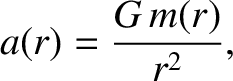
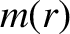 is the mass enclosed by the surface.
Now, if
is the mass enclosed by the surface.
Now, if 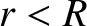 then
then
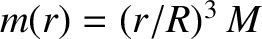 (by proportion), but if
(by proportion), but if 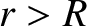 then
then 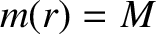 . Thus, we
deduce that
. Thus, we
deduce that

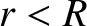 , and
for
, and
for 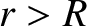 .
In other words, inside the Earth, the gravitational acceleration due to the Earth increases linearly with distance from the
Earth's center, but, outside the Earth, it falls off as the inverse-square of distance from the
Earth's center. In particular, the gravitational field outside the Earth is exactly the
same as that of a point object whose mass is equal to that of the Earth, and that is located at the
Earth's center. This is an example of an important result first derived by Newton; namely, that the
gravitational field outside a spherically symmetric mass distribution is the same as that of a
point object located at the center of the distribution whose mass is equal to that of the distribution.
.
In other words, inside the Earth, the gravitational acceleration due to the Earth increases linearly with distance from the
Earth's center, but, outside the Earth, it falls off as the inverse-square of distance from the
Earth's center. In particular, the gravitational field outside the Earth is exactly the
same as that of a point object whose mass is equal to that of the Earth, and that is located at the
Earth's center. This is an example of an important result first derived by Newton; namely, that the
gravitational field outside a spherically symmetric mass distribution is the same as that of a
point object located at the center of the distribution whose mass is equal to that of the distribution.

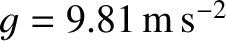 ,
and that the measured (mean) radius of the Earth is
,
and that the measured (mean) radius of the Earth is
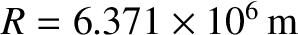 , we arrive at the
following estimate for the Earth's mass,
, we arrive at the
following estimate for the Earth's mass,
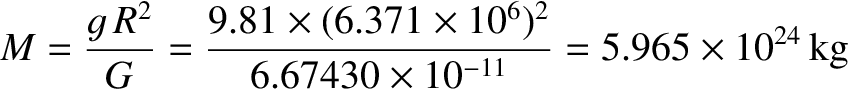
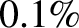 of the correct value, which is
of the correct value, which is