Next: Gravitational Field of Earth Up: Newtonian Gravity Previous: Gravity
Suppose that we have an isolated point source that emits an incompressible fluid isotropically in all directions at
the rate
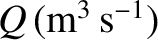 . By symmetry, we would expect the fluid to flow radially away from the source, isotropically in all directions. In other words, if the source is located at the origin then we expect the fluid
velocity at displacement
. By symmetry, we would expect the fluid to flow radially away from the source, isotropically in all directions. In other words, if the source is located at the origin then we expect the fluid
velocity at displacement  to be of the form
to be of the form
 . See Figure 1.11. The net volume rate of
flow of fluid out of the surface is
. See Figure 1.11. The net volume rate of
flow of fluid out of the surface is
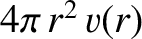 . However, if the fluid is incompressible (and the flow pattern
has achieved a steady-state) then the volume rate of flow out of the surface must equal the volume rate of
flow from the source (otherwise, the fluid inside the surface would suffer compression or rarefaction). In other words,
. However, if the fluid is incompressible (and the flow pattern
has achieved a steady-state) then the volume rate of flow out of the surface must equal the volume rate of
flow from the source (otherwise, the fluid inside the surface would suffer compression or rarefaction). In other words,
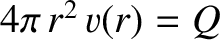 . Hence, Equation (1.242) becomes
. Hence, Equation (1.242) becomes
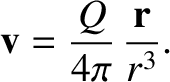 |
(1.243) |
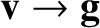 and
and
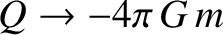 .
.
Suppose that we have  point sources of incompressible fluid. Let the
point sources of incompressible fluid. Let the  th source have a volume rate of
flow
th source have a volume rate of
flow  . Let us surround these sources by an imaginary closed surface (that is
not necessarily spherical),
. Let us surround these sources by an imaginary closed surface (that is
not necessarily spherical),  . Now, the volume rate of flow of fluid out of
. Now, the volume rate of flow of fluid out of  is
is
 , where
, where
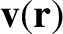 is the flow field, and
is the flow field, and 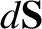 is an (outward pointing) element of
is an (outward pointing) element of  . (See Section A.16.) However, if the fluid is incompressible (and the flow pattern
has achieved a steady-state) then the volume rate of flow out of
. (See Section A.16.) However, if the fluid is incompressible (and the flow pattern
has achieved a steady-state) then the volume rate of flow out of  must match the sum of the volume
rates of flow of the sources within
must match the sum of the volume
rates of flow of the sources within  (otherwise, the fluid inside the surface would suffer compression or rarefaction). Thus, we deduce that
(otherwise, the fluid inside the surface would suffer compression or rarefaction). Thus, we deduce that
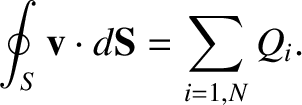 |
(1.244) |
 then they do not affect the previous relation (because
a source outside
then they do not affect the previous relation (because
a source outside  gives rise to zero net flow of incompressible fluid out of
gives rise to zero net flow of incompressible fluid out of  ). Hence,
we can interpret the sum in the previous equation as a sum that includes all sources that lie inside
). Hence,
we can interpret the sum in the previous equation as a sum that includes all sources that lie inside  , but excludes any sources that lie outside
, but excludes any sources that lie outside  .
.
Finally, we can exploit the previously mentioned analogy between incompressible fluid flow and gravitational acceleration to
deduce the following result. Suppose that there are  point objects of mass
point objects of mass 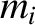 . Let us surround these objects by an imaginary surface
. Let us surround these objects by an imaginary surface  . Making use of the
identifications
. Making use of the
identifications
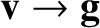 and
and
 , the previous equation
transforms to give
, the previous equation
transforms to give
 then they do not affect the previous relation. Thus, we deduce that
the flux of gravitational acceleration out of an arbitrary closed surface,
then they do not affect the previous relation. Thus, we deduce that
the flux of gravitational acceleration out of an arbitrary closed surface,  , is equal to
, is equal to 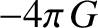 multiplied
by the sum of the masses of any objects lying inside the surface. This is Gauss's law. The imaginary surface
multiplied
by the sum of the masses of any objects lying inside the surface. This is Gauss's law. The imaginary surface  is known as a Gaussian surface.
is known as a Gaussian surface.
Suppose that, instead of having a collection of point objects, we have a continuous mass distribution whose
mass density is
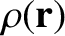 . The previous equation generalizes to give
. The previous equation generalizes to give
 is the volume enclosed by
is the volume enclosed by  , and
, and 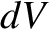 is an element of
is an element of  . (See Section A.17.)
Now, according to the divergence theorem (see Section A.20),
. (See Section A.17.)
Now, according to the divergence theorem (see Section A.20),
 |
(1.247) |
 is the
divergence of the acceleration field. The previous two equations yield
is the
divergence of the acceleration field. The previous two equations yield
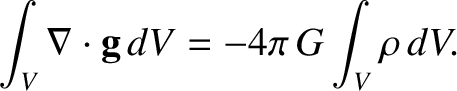 |
(1.248) |
 is arbitrary, so the only way that the previous equation could hold for all
possible volumes is if
This is the differential form of Gauss's law.
is arbitrary, so the only way that the previous equation could hold for all
possible volumes is if
This is the differential form of Gauss's law.