Making use of Equations (1.329), (1.349), (1.354), (1.364), and (1.365), the combined
gravitational and centrifugal potential outside the Earth is
![$\displaystyle {\mit\Phi}+\chi = -\frac{G\,M}{R}\left[\frac{R}{r} -\frac{3\,\zet...
...\sin^2\theta + \frac{3\,\zeta}{2}\left(\frac{r}{R}\right)^2\sin^2\theta\right].$](img901.png) |
(1.369) |
According to Equations (1.328), (1.329), and (1.364), the surface of the Earth lies at radius
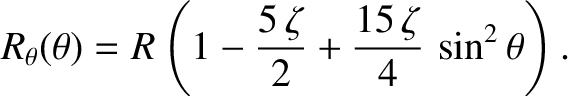 |
(1.370) |
The effective gravitational acceleration at the Earth's surface is
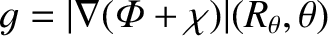 , which
reduces to
, which
reduces to
![$\displaystyle g(\lambda) = \frac{G\,M}{R^2}\left[1+\frac{\zeta}{2} - \frac{15\,\zeta}{4}\,\cos^2\lambda + {\cal O}(\zeta^2)\right],$](img904.png) |
(1.371) |
where
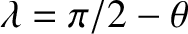 corresponds to terrestrial latitude. The previous expression shows that the Earth's
rotation, combined with its equatorial bulge, causes the acceleration experienced by objects close to the Earth's
surface, that co-rotate with the Earth, to vary slightly with latitude. The acceleration is greatest at the poles (
corresponds to terrestrial latitude. The previous expression shows that the Earth's
rotation, combined with its equatorial bulge, causes the acceleration experienced by objects close to the Earth's
surface, that co-rotate with the Earth, to vary slightly with latitude. The acceleration is greatest at the poles (
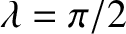 ), and weakest at the equator (
), and weakest at the equator (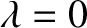 ).
To be more exact, we predict that
).
To be more exact, we predict that
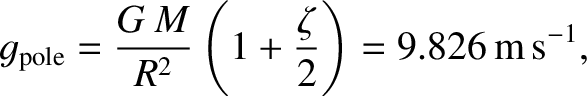 |
(1.372) |
and
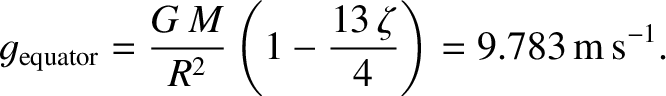 |
(1.373) |
In fact, the true values of the polar and equatorial accelerations are
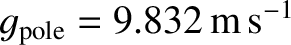 and
and
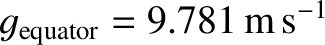 , respectively.
, respectively.
![$\displaystyle {\mit\Phi}+\chi = -\frac{G\,M}{R}\left[\frac{R}{r} -\frac{3\,\zet...
...\sin^2\theta + \frac{3\,\zeta}{2}\left(\frac{r}{R}\right)^2\sin^2\theta\right].$](img901.png)
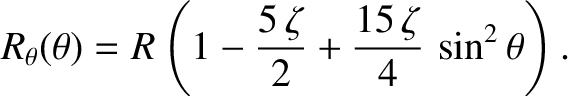
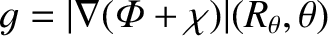 , which
reduces to
, which
reduces to
![$\displaystyle g(\lambda) = \frac{G\,M}{R^2}\left[1+\frac{\zeta}{2} - \frac{15\,\zeta}{4}\,\cos^2\lambda + {\cal O}(\zeta^2)\right],$](img904.png)
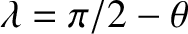 corresponds to terrestrial latitude. The previous expression shows that the Earth's
rotation, combined with its equatorial bulge, causes the acceleration experienced by objects close to the Earth's
surface, that co-rotate with the Earth, to vary slightly with latitude. The acceleration is greatest at the poles (
corresponds to terrestrial latitude. The previous expression shows that the Earth's
rotation, combined with its equatorial bulge, causes the acceleration experienced by objects close to the Earth's
surface, that co-rotate with the Earth, to vary slightly with latitude. The acceleration is greatest at the poles (
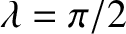 ), and weakest at the equator (
), and weakest at the equator (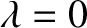 ).
To be more exact, we predict that
).
To be more exact, we predict that
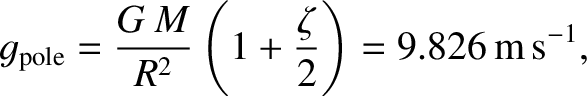
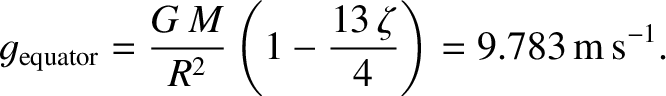
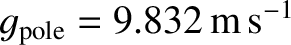 and
and
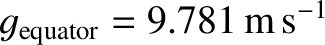 , respectively.
, respectively.