Next: Gravitational Torque on Axisymmetric Up: Spheroidal Mass Distributions Previous: Surface Gravity of Earth
 -axis corresponds to the spheroid's rotation axis.
-axis corresponds to the spheroid's rotation axis.
It is clear, by symmetry, that the  -,
-,  -, and
-, and  -axes are principal axes of rotation. (See Section 1.7.2.)
Hence, given that
-axes are principal axes of rotation. (See Section 1.7.2.)
Hence, given that
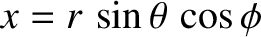 ,
,
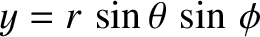 ,
,
 , where
, where  ,
,  ,
,  are conventional spherical coordinates (see Section A.23), the principal moments of inertia of the spheroid are
are conventional spherical coordinates (see Section A.23), the principal moments of inertia of the spheroid are
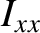 |
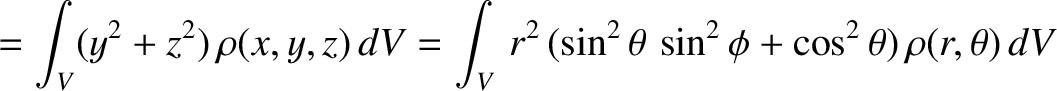 |
|
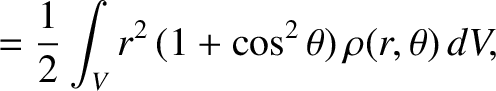 |
(1.374) | |
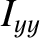 |
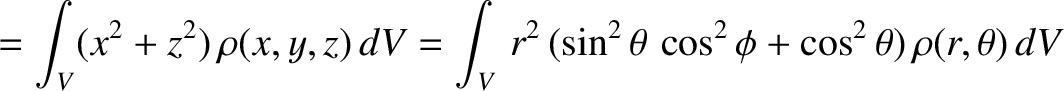 |
|
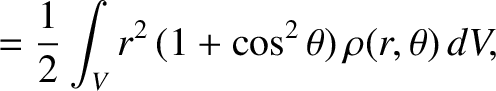 |
(1.375) | |
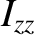 |
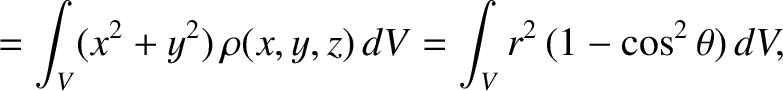 |
(1.376) |
 , of the spheroid. In writing the previous formulae, we have made use
of the fact that the mass density of the spheroid,
, of the spheroid. In writing the previous formulae, we have made use
of the fact that the mass density of the spheroid,
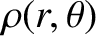 , is independent of the azimuthal angle,
, is independent of the azimuthal angle,  , and
that the averages of
, and
that the averages of
 and
and
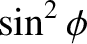 over the volume of a mass distribution that is independent of
over the volume of a mass distribution that is independent of  are
both equal to
are
both equal to  .
.
Let us write
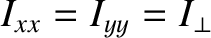 and
and
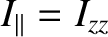 . (See Section 1.7.2.) Now, according to Equations (1.332)–(1.334), the mass density of the spheroid
is
. (See Section 1.7.2.) Now, according to Equations (1.332)–(1.334), the mass density of the spheroid
is
 |
(1.377) |
![$\displaystyle \rho_0(r) =\left\{\begin{array}{lll}\gamma&~~~~&r\leq R\\ [0.5ex]0&&r>R\end{array}\right..$](img924.png) |
(1.378) |
 is the mean radius of the spheroid, and
is the mean radius of the spheroid, and  is its uniform mass density.
Given that
is its uniform mass density.
Given that
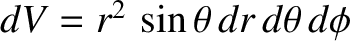 , we can evaluate the integrals (1.374)–(1.376) to
give
, we can evaluate the integrals (1.374)–(1.376) to
give
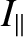 |
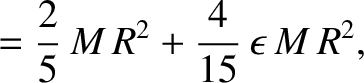 |
(1.379) |
 |
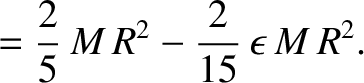 |
(1.380) |
 is the mass of the spheroid.
is the mass of the spheroid.
If we apply the previous two results to the Earth, for which
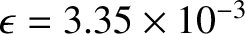 (see Section 1.10.2), then
it is clear that the slight rotational flattening of the Earth along its axis of diurnal rotation causes the principal moment
of inertia about this axis,
(see Section 1.10.2), then
it is clear that the slight rotational flattening of the Earth along its axis of diurnal rotation causes the principal moment
of inertia about this axis,
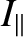 , to be slightly larger that the principal moment of inertia,
, to be slightly larger that the principal moment of inertia, 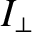 , about an
axis that lies in the Earth's equatorial plane.
In particular,
, about an
axis that lies in the Earth's equatorial plane.
In particular,
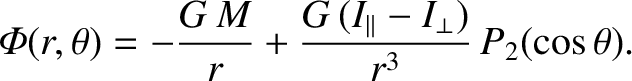 |
(1.382) |