Consider an axisymmetric mass distribution. Let us set up a Cartesian coordinate system whose origin
corresponds to the center of mass of the distribution, and whose  -axis corresponds to the symmetry axis.
The fact that the origin corresponds to the center of mass implies that
-axis corresponds to the symmetry axis.
The fact that the origin corresponds to the center of mass implies that
 |
(1.383) |
 , of the distribution, and
, of the distribution, and 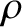 is the distribution's mass density. (See Section 1.4.2.) By symmetry, the Cartesian axes are principal axes of rotation, which implies that all of the products
of inertia are zero. (See Section 1.7.2.) In other words,
is the distribution's mass density. (See Section 1.4.2.) By symmetry, the Cartesian axes are principal axes of rotation, which implies that all of the products
of inertia are zero. (See Section 1.7.2.) In other words,
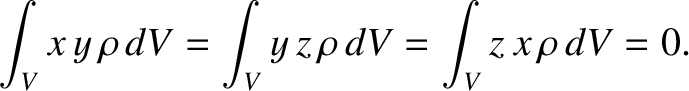 |
(1.384) |
Finally, the principal moments of inertia of the distribution are
Suppose that the mass distribution lies in the gravitational field of a distant object. Let
 be the gravitational potential generated by the distant object. The gravitational torque, about the center of mass, that the
distant object exerts on the mass distribution is
be the gravitational potential generated by the distant object. The gravitational torque, about the center of mass, that the
distant object exerts on the mass distribution is
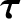 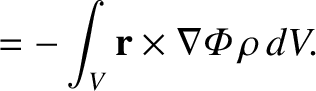 |
(1.387) |
[See Section 1.4.5 and Equation (1.269).]
However, we expect
 to only vary slightly across the mass distribution, assuming that the
distance of the distant object from the origin is much larger than the dimensions of the
mass distribution. Thus, we can Taylor expand
to only vary slightly across the mass distribution, assuming that the
distance of the distant object from the origin is much larger than the dimensions of the
mass distribution. Thus, we can Taylor expand
 about the origin to give
about the origin to give
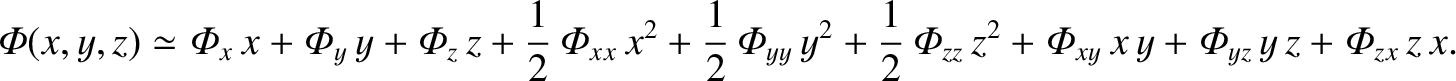 |
(1.388) |
Here,
 denotes
denotes
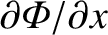 evaluated at the origin, whereas
evaluated at the origin, whereas
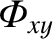 denotes
denotes
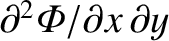 evaluated at the origin, et cetera. Note that we have set the
value of
evaluated at the origin, et cetera. Note that we have set the
value of
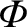 at the origin to zero, as we are free to do, given that gravitational potential (like
gravitational potential energy) is undefined to an arbitrary additive constant.
The previous six equations can be combined to give
We conclude that the distant object exerts a torque on the mass distribution whose direction lies in the distribution's equatorial plane.
Note, however, that the distant object is incapable of exerting a torque on a spherically symmetric mass distribution (i.e.,
a distribution for which
at the origin to zero, as we are free to do, given that gravitational potential (like
gravitational potential energy) is undefined to an arbitrary additive constant.
The previous six equations can be combined to give
We conclude that the distant object exerts a torque on the mass distribution whose direction lies in the distribution's equatorial plane.
Note, however, that the distant object is incapable of exerting a torque on a spherically symmetric mass distribution (i.e.,
a distribution for which
 ).
).
 -axis corresponds to the symmetry axis.
The fact that the origin corresponds to the center of mass implies that
-axis corresponds to the symmetry axis.
The fact that the origin corresponds to the center of mass implies that

 , of the distribution, and
, of the distribution, and 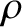 is the distribution's mass density. (See Section 1.4.2.) By symmetry, the Cartesian axes are principal axes of rotation, which implies that all of the products
of inertia are zero. (See Section 1.7.2.) In other words,
is the distribution's mass density. (See Section 1.4.2.) By symmetry, the Cartesian axes are principal axes of rotation, which implies that all of the products
of inertia are zero. (See Section 1.7.2.) In other words,
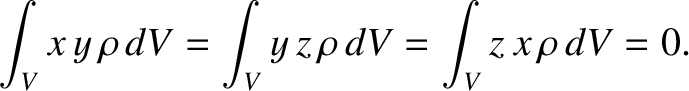
 be the gravitational potential generated by the distant object. The gravitational torque, about the center of mass, that the
distant object exerts on the mass distribution is
be the gravitational potential generated by the distant object. The gravitational torque, about the center of mass, that the
distant object exerts on the mass distribution is
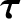
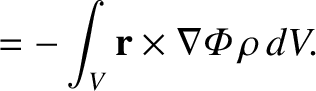
 to only vary slightly across the mass distribution, assuming that the
distance of the distant object from the origin is much larger than the dimensions of the
mass distribution. Thus, we can Taylor expand
to only vary slightly across the mass distribution, assuming that the
distance of the distant object from the origin is much larger than the dimensions of the
mass distribution. Thus, we can Taylor expand
 about the origin to give
about the origin to give
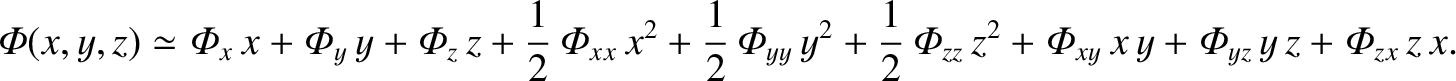
 denotes
denotes
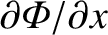 evaluated at the origin, whereas
evaluated at the origin, whereas
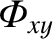 denotes
denotes
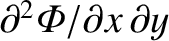 evaluated at the origin, et cetera. Note that we have set the
value of
evaluated at the origin, et cetera. Note that we have set the
value of
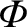 at the origin to zero, as we are free to do, given that gravitational potential (like
gravitational potential energy) is undefined to an arbitrary additive constant.
The previous six equations can be combined to give
We conclude that the distant object exerts a torque on the mass distribution whose direction lies in the distribution's equatorial plane.
Note, however, that the distant object is incapable of exerting a torque on a spherically symmetric mass distribution (i.e.,
a distribution for which
at the origin to zero, as we are free to do, given that gravitational potential (like
gravitational potential energy) is undefined to an arbitrary additive constant.
The previous six equations can be combined to give
We conclude that the distant object exerts a torque on the mass distribution whose direction lies in the distribution's equatorial plane.
Note, however, that the distant object is incapable of exerting a torque on a spherically symmetric mass distribution (i.e.,
a distribution for which
 ).
).