Next: Spacetime Interval Up: Theoretical Basis of Special Previous: Galilean Transformation
 , at time
, at time  , the origin of the
, the origin of the 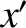 -axis is located a perpendicular
distance
-axis is located a perpendicular
distance  from the origin of the
from the origin of the  -axis. Moreover, in
-axis. Moreover, in  , our event is located a perpendicular distance
, our event is located a perpendicular distance 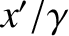 from
the origin of the
from
the origin of the 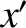 -axis, because of length contraction. [See Equation (3.81).] Thus,
-axis, because of length contraction. [See Equation (3.81).] Thus,
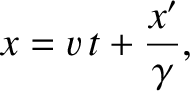 |
(3.95) |
 |
(3.96) |
 -direction or the
-direction or the  -direction, and because there is no contraction of
lengths perpendicular to the
-direction, and because there is no contraction of
lengths perpendicular to the  -axis, we deduce that
-axis, we deduce that
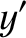 |
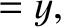 |
(3.97) |
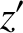 |
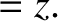 |
(3.98) |
 , a clock located at the origin reads
, a clock located at the origin reads 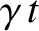 when a clock at the origin of
when a clock at the origin of  reads
reads  , as
a consequence of time dilation (note that, in
, as
a consequence of time dilation (note that, in  , a clock in
, a clock in  appears to run slowly by a factor
appears to run slowly by a factor  ). [See Equation (3.73).] Furthermore, a second clock in
). [See Equation (3.73).] Furthermore, a second clock in  , displaced from the origin a distance
, displaced from the origin a distance  (measured in
(measured in  ) in the
) in the  -direction,
appears to read
-direction,
appears to read
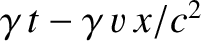 as a consequence of clock error. [See Equation (3.87).] Hence,
as a consequence of clock error. [See Equation (3.87).] Hence,
 |
(3.99) |
We deduce that the transformation of coordinates that is consistent with the theory of relativity is
This transformation is know as the Lorentz transformation. Note that, in the limit in which the relative velocity of frames and
and  is non-relativistic (i.e., much smaller in magnitude than the speed of light in vacuum), so that
is non-relativistic (i.e., much smaller in magnitude than the speed of light in vacuum), so that 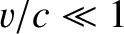 , and
, and
 , the Lorentz transformation
morphs into the Galilean transformation, (3.88)–(3.91). Thus, the common sense transformation, (3.88)–(3.91), holds as long as the relative velocity between the two frames of reference is much
smaller than the velocity of light in vacuum.
Incidentally, it is easily shown from Equations (3.100)–(3.103) that
, the Lorentz transformation
morphs into the Galilean transformation, (3.88)–(3.91). Thus, the common sense transformation, (3.88)–(3.91), holds as long as the relative velocity between the two frames of reference is much
smaller than the velocity of light in vacuum.
Incidentally, it is easily shown from Equations (3.100)–(3.103) that
In the Galilean transformation, (3.88)–(3.91), the transformation of time is completely independent from that of space. This is no longer the case in the Lorentz transformation, (3.100)–(3.103). In fact, the transformations of space and time are mixed together in special relativity in such a manner that, rather than thinking of space and time as separate concepts, it makes more sense to talk about a generalized concept that Einstein called spacetime.