Next: Transformation of Velocity Up: Theoretical Basis of Special Previous: Lorentz Transformation
 and
and 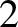 , whose spacetime coordinates in some inertial frame
, whose spacetime coordinates in some inertial frame  are (
are (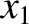 ,
, 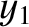 ,
, 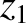 ,
, 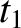 ) and (
) and (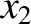 ,
, 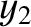 ,
, 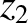 ,
, 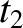 ), respectively. Let us form the differences between these coordinates,
), respectively. Let us form the differences between these coordinates,
 ,
,
 ,
,
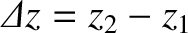 , and
, and
 . The spatial distance,
. The spatial distance,
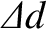 , between the
two events is written
, between the
two events is written
Suppose that we shift the origin of our coordinate system in  . It is obvious that this process does not change
the distance between our two events. In other words,
. It is obvious that this process does not change
the distance between our two events. In other words,
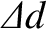 is invariant under a shift of the origin of the
coordinate system, as is easily verified.
Suppose that we rotate our coordinate axes in
is invariant under a shift of the origin of the
coordinate system, as is easily verified.
Suppose that we rotate our coordinate axes in  . (See Section A.5.) Such a process is length-preserving. In other words,
. (See Section A.5.) Such a process is length-preserving. In other words,
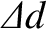 is invariant under a rotation of the coordinate axes, as is easily verified.
However, it is evident, by inspection, that
is invariant under a rotation of the coordinate axes, as is easily verified.
However, it is evident, by inspection, that
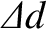 is not invariant under a Lorentz transformation. Let us try to find a quantity that is invariant.
is not invariant under a Lorentz transformation. Let us try to find a quantity that is invariant.
Consider a second inertial frame,  , that moves with velocity
, that moves with velocity
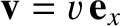 with respect to
with respect to  , and is also
in a standard configuration with respect to
, and is also
in a standard configuration with respect to  . Let events
. Let events  and
and  have spacetime coordinates (
have spacetime coordinates (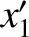 ,
, 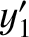 ,
, 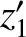 ,
, 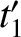 ) and (
) and (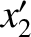 ,
, 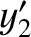 ,
, 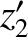 ,
, 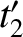 ), respectively, in
), respectively, in  . Let us again form the differences between these coordinates,
. Let us again form the differences between these coordinates,
 ,
,
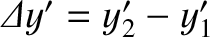 ,
,
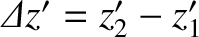 , and
, and
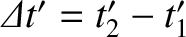 .
The spacetime interval between events 1 and 2 in
.
The spacetime interval between events 1 and 2 in  is defined
is defined
 is
is
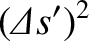 |
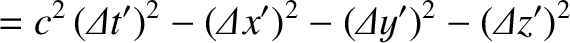 |
|
![$\displaystyle = \gamma^2\left[c^2\,({\mit\Delta}t)^2-2\,v\,{\mit\Delta x}\,{\mi...
...Delta}x)^2-2\,v\,{\mit\Delta x}\,{\mit\Delta t}+ v^2\,({\mit\Delta t})^2\right]$](img2485.png) |
||
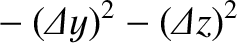 |
||
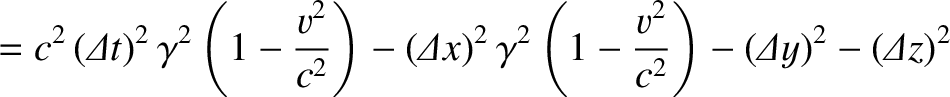 |
||
 |
||
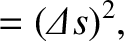 |
(3.114) |
 is
is
![$\displaystyle \frac{{\mit\Delta}d}{{\mit\Delta t}}= c\left[1-\frac{({\mit\Delta} s)^2}{(c\,{\mit\Delta} t)^2}\right]^{1/2},$](img2490.png) |
(3.115) |
 . Hence, we deduce that
. Hence, we deduce that
 |
(3.116) |
 is
is
 . Now, the
speed of the light ray in
. Now, the
speed of the light ray in  is
is
![$\displaystyle \frac{{\mit\Delta}d'}{{\mit\Delta t'}}= c\left[1-\frac{({\mit\Delta} s')^2}{(c\,{\mit\Delta} t')^2}\right]^{1/2} = c.$](img2493.png) |
(3.117) |
 in all inertial frames of reference.
in all inertial frames of reference.