Next: Causality Up: Theoretical Basis of Special Previous: Spacetime Interval
 , that moves at the fixed (subluminal) velocity
, that moves at the fixed (subluminal) velocity
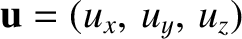 .
Suppose that the particle is located at the origin at time
.
Suppose that the particle is located at the origin at time  . It follows that, at time
. It follows that, at time  , the particle is located at point
, the particle is located at point
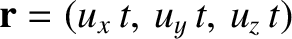 . Let us observe the motion of the particle in a second inertial frame,
. Let us observe the motion of the particle in a second inertial frame,  , that moves with (subluminal) velocity
, that moves with (subluminal) velocity
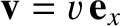 with respect to
with respect to  , and is in a standard configuration with respect to
, and is in a standard configuration with respect to  . It follows from
Equations (3.100)–(3.103) that the particle is located at the origin of
. It follows from
Equations (3.100)–(3.103) that the particle is located at the origin of  at
at 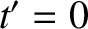 . The location of the
particle in
. The location of the
particle in  , at time
, at time 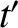 , can be written
, can be written
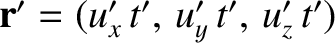 , where
, where
 is the
particle's velocity in
is the
particle's velocity in  . It follows from
Equations (3.100)–(3.103) that
. It follows from
Equations (3.100)–(3.103) that
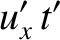 |
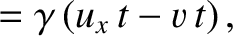 |
(3.118) |
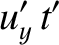 |
 |
(3.119) |
 |
 |
(3.120) |
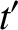 |
 |
(3.121) |
Let
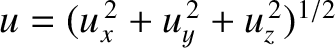 and
and
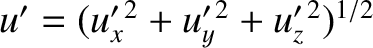 be the speeds of the
particle in frames
be the speeds of the
particle in frames  and
and  , respectively. It is easily demonstrated, from the transformation of velocity, that
, respectively. It is easily demonstrated, from the transformation of velocity, that
 and
and 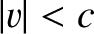 then the right-hand side is positive, implying that
then the right-hand side is positive, implying that  . In other words, the resultant of two subluminal velocities is another subluminal velocity. It is evident that a particle can never attain the velocity of light relative to a given inertial frame, no matter how many subluminal velocity increments it is given. It follows that no inertial frame can ever appear to propagate with a superluminal velocity with respect to any other inertial frame (because we can track a given inertial frame in terms of a particle that remains at rest at the origin of that frame).
Of course, if
. In other words, the resultant of two subluminal velocities is another subluminal velocity. It is evident that a particle can never attain the velocity of light relative to a given inertial frame, no matter how many subluminal velocity increments it is given. It follows that no inertial frame can ever appear to propagate with a superluminal velocity with respect to any other inertial frame (because we can track a given inertial frame in terms of a particle that remains at rest at the origin of that frame).
Of course, if 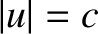 then
then  . In other words, a particle traveling at the speed of light in one inertial frame does so
in all inertial frames.
. In other words, a particle traveling at the speed of light in one inertial frame does so
in all inertial frames.
It is evident from Equation (3.125) that there is only a single speed—namely,  —that is the same in all inertial frames of reference. Now, according to Einstein's first postulate, any wave that propagates in the absence of a physical medium must propagate at the same speed in all inertial frames of
reference, otherwise the different wave speeds in different reference frames could be used to distinguish
between the frames. Hence, we deduce that all waves that propagate in the absence of a physical medium (e.g., a gas, liquid, or solid) must propagate
at the common speed
—that is the same in all inertial frames of reference. Now, according to Einstein's first postulate, any wave that propagates in the absence of a physical medium must propagate at the same speed in all inertial frames of
reference, otherwise the different wave speeds in different reference frames could be used to distinguish
between the frames. Hence, we deduce that all waves that propagate in the absence of a physical medium (e.g., a gas, liquid, or solid) must propagate
at the common speed  in all inertial reference frames. Thus, gravitational waves, which are ripples in the fabric
of spacetime, must travel at the same speed,
in all inertial reference frames. Thus, gravitational waves, which are ripples in the fabric
of spacetime, must travel at the same speed,  , as electromagnetic waves, because both waves propagate in the
absence of media. Thus, we could just as well designate
, as electromagnetic waves, because both waves propagate in the
absence of media. Thus, we could just as well designate  as the speed of gravitational waves.
as the speed of gravitational waves.
Note, finally, that the Lorentz transformation is the only (linear) transformation of coordinates that preserves the speed  , and
morphs into the tried and tested Galilean transformation in the limit that
, and
morphs into the tried and tested Galilean transformation in the limit that 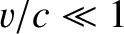 . In fact, it is possible to
guess the form of the Lorentz transformation by searching for a (linear) coordinate transformation that has these
two properties.
. In fact, it is possible to
guess the form of the Lorentz transformation by searching for a (linear) coordinate transformation that has these
two properties.