Next: Relativistic Aberration of Light Up: Theoretical Basis of Special Previous: Transformation of Velocity
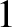 and
and 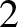 have spacetime coordinates (
have spacetime coordinates (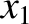 , 0, 0,
, 0, 0, 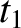 ) and (
) and (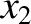 , 0, 0,
, 0, 0, 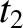 ) in some inertial
reference frame,
) in some inertial
reference frame, 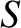 . Suppose that event
. Suppose that event 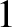 causes event
causes event 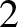 . It follows that
. It follows that 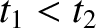 . In other words, event
. In other words, event 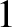 necessarily precedes event
necessarily precedes event 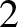 in time. Let
in time. Let
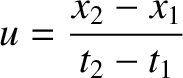 |
(3.126) |
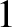 to event
to event 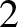 in order to allow the former event to cause the latter. Let us observe the two events in a second inertial frame,
in order to allow the former event to cause the latter. Let us observe the two events in a second inertial frame, 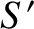 , that moves at velocity
, that moves at velocity
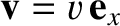 with respect to
with respect to 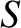 , and is in a standard configuration with respect to
, and is in a standard configuration with respect to 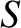 .
According to Equation (3.103),
.
According to Equation (3.103),
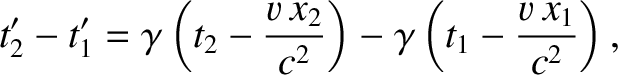 |
(3.127) |
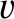 , whose magnitude can never exceed
, whose magnitude can never exceed 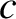 , event
, event 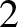 can never occur prior to event
can never occur prior to event
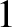 in
in 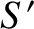 , otherwise we could classify inertial frames into two groups; those in which event
, otherwise we could classify inertial frames into two groups; those in which event 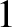 appears to cause event
appears to cause event 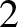 , and
those in which event
, and
those in which event 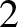 appears to cause event
appears to cause event 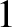 . However, this state of affairs is forbidden by Einstein's first postulate.
Thus, we require
. However, this state of affairs is forbidden by Einstein's first postulate.
Thus, we require
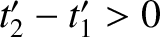 for all
for all 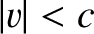 . It is clear from Equation (3.128) that this is only possible if
. It is clear from Equation (3.128) that this is only possible if 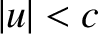 . Hence, we deduce that
information can never propagate faster than the speed of light in vacuum, in any inertial reference frame, otherwise it is possible to find other inertial reference frames in which causality appears to be violated.
. Hence, we deduce that
information can never propagate faster than the speed of light in vacuum, in any inertial reference frame, otherwise it is possible to find other inertial reference frames in which causality appears to be violated.