Next: Relativistic Beaming of Light Up: Theoretical Basis of Special Previous: Causality
Consider a light ray that travels from a distant source to an observer located at the origin of some inertial frame,  . Let
. Let 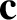 be the phase velocity of the light ray. Of course,
be the phase velocity of the light ray. Of course,
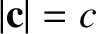 , where
, where  is the speed of light in vacuum. Suppose that
is the speed of light in vacuum. Suppose that 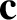 lies in the
lies in the  -
- plane, such that its direction subtends an angle
plane, such that its direction subtends an angle  with the
with the 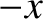 -direction, as
shown in Figure 3.10. It is clear from the figure that
-direction, as
shown in Figure 3.10. It is clear from the figure that
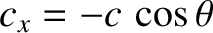 and
and
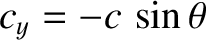 .
Suppose that a second observer, moving with velocity
.
Suppose that a second observer, moving with velocity
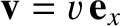 with respect to the first, observes the
light ray. Let
with respect to the first, observes the
light ray. Let 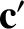 be the phase velocity of the light ray in the second observer's frame,
be the phase velocity of the light ray in the second observer's frame,  , which is in a standard configuration with respect to frame
, which is in a standard configuration with respect to frame  . Of course,
. Of course,
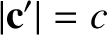 . Suppose that
. Suppose that 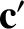 lies in the
lies in the 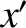 -
-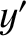 plane, such that its direction subtends an angle
plane, such that its direction subtends an angle  with the
with the 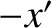 -direction, as
shown in Figure 3.10. It is clear from the figure that
-direction, as
shown in Figure 3.10. It is clear from the figure that
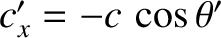 and
and
 .
The transformation of velocity, (3.122)–(3.124), yields
.
The transformation of velocity, (3.122)–(3.124), yields
 |
(3.129) |
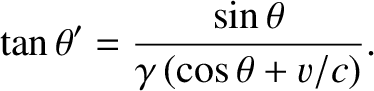 |
(3.130) |
In particular, suppose that the first observer is located in the rest frame of the Sun, and the second is located on the Earth, whose
instantaneous orbital velocity about the Sun is
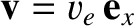 , where
, where
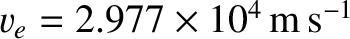 . In this case, the
previous equation yields
. In this case, the
previous equation yields
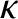 |
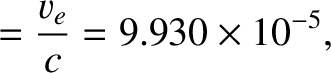 |
(3.132) |
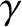 |
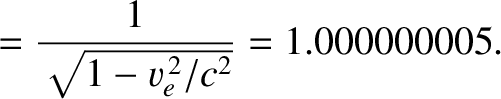 |
(3.133) |