Next: Light Propagation through Dielectric Up: Theoretical Basis of Special Previous: Relativistic Aberration of Light
Consider a point source that emits light isotropically in all directions in its rest frame,  Let us observe
this source in a frame of reference,
Let us observe
this source in a frame of reference,  , that moves with velocity
, that moves with velocity
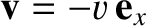 , and is in a standard configuration, with respect to frame
, and is in a standard configuration, with respect to frame  . Thus, the
source appears to move with velocity
. Thus, the
source appears to move with velocity
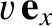 in frame
in frame  . See Figure 3.11. Now, half of the emitted
radiation in
. See Figure 3.11. Now, half of the emitted
radiation in  emerges in the region
emerges in the region  , bounded by the rays
, bounded by the rays  and
and  shown in the figure. Likewise, half the emitted
radiation in
shown in the figure. Likewise, half the emitted
radiation in  emerges in the region
emerges in the region  , bounded by the rays
, bounded by the rays  and
and  shown in the figure. Ray
shown in the figure. Ray
 has the phase velocity
has the phase velocity
 . Likewise, ray
. Likewise, ray  has the phase velocity
has the phase velocity
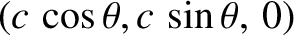 ,
where the angle
,
where the angle  is shown in the figure. By symmetry, the angle subtended between
is shown in the figure. By symmetry, the angle subtended between  and
and 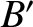 is
the same as that subtended between
is
the same as that subtended between  and
and 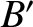 .
The transformation of velocity, (3.122)–(3.124), yields
.
The transformation of velocity, (3.122)–(3.124), yields
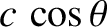 |
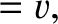 |
(3.134) |
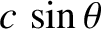 |
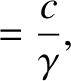 |
(3.135) |
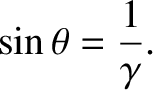 |
(3.136) |
 , half of the emitted radiation is beamed into
a cone whose axis is
, half of the emitted radiation is beamed into
a cone whose axis is  , and whose half-angle is
, and whose half-angle is
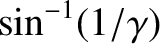 . If the source is moving very close to the
velocity of light then
. If the source is moving very close to the
velocity of light then
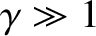 , and
, and
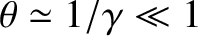 . In other words, the emitted radiation is
beamed very strongly in the direction of motion of the source.
. In other words, the emitted radiation is
beamed very strongly in the direction of motion of the source.