Next: Relativistic Dynamics Up: Theoretical Basis of Special Previous: Relativistic Beaming of Light
 be the refractive index of the medium.
Thus, in the rest frame,
be the refractive index of the medium.
Thus, in the rest frame,  , of the medium, light propagates at the phase velocity
, of the medium, light propagates at the phase velocity 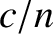 . Let us transform to a frame of
reference,
. Let us transform to a frame of
reference,  , that moves at velocity
, that moves at velocity
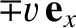 , and is in a standard configuration, with respect to frame
, and is in a standard configuration, with respect to frame  . Thus, the
medium appears to flow at the velocity
. Thus, the
medium appears to flow at the velocity
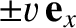 in frame
in frame  .
According to Equation (3.122), the phase velocity of light propagating in the
.
According to Equation (3.122), the phase velocity of light propagating in the  -direction in frame
-direction in frame  , in which the medium
flows at velocity
, in which the medium
flows at velocity
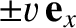 , is
, is
 |
(3.137) |
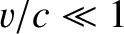 ,
the previous equation reduces to
,
the previous equation reduces to
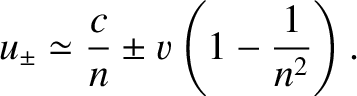 |
(3.138) |