Maxwell's Equations
We are now in a position to write out a complete, mathematically self-consistent, set of field equations that govern
electric and magnetic phenomena:
The equations are known as Maxwell's equation. The first Maxwell equation describes
how electric fields are induced by electric charges, and is
equivalent to Gauss's law. The second Maxwell equation states that there
is no such thing as a magnetic monopole. The third Maxwell equation describes the induction
of electric fields by changing magnetic fields, and is equivalent to Faraday's law of electromagnetic induction.
The fourth Maxwell equation describes
the generation of magnetic fields by electric currents, and the induction of
magnetic fields by changing electric fields, and incorporates Ampère's circuital law.
As an example of a calculation involving the displacement current,
let us find the current and displacement current densities associated with the
decaying charge distribution
 |
(2.488) |
where  is a spherical polar coordinate (see Section A.23),
is a spherical polar coordinate (see Section A.23), 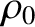 is a constant, and
is a constant, and 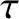 and
and 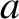 are positive constants.
Now, according to charge conservation,
are positive constants.
Now, according to charge conservation,
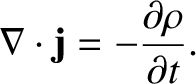 |
(2.489) |
[See Equation (2.473).]
By symmetry, we expect
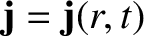 . Hence, it follows that
. Hence, it follows that
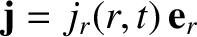 [because only a radial current has a non-zero
divergence when
[because only a radial current has a non-zero
divergence when
 ]. [See Equation (A.173).] Thus, the previous two equations
yield.
]. [See Equation (A.173).] Thus, the previous two equations
yield.
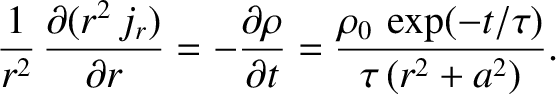 |
(2.490) |
The previous expression can be integrated, subject to the sensible boundary condition
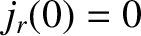 , to give
, to give
![$\displaystyle j_r(r) = \frac{\rho_0}{\tau}\,{\rm e}^{-t/\tau}\left[\frac{r-a\,\tan^{-1}(r/a)}{r^2}\right].$](img2078.png) |
(2.491) |
Now, the electric field generated by the decaying charge
distribution satisfies
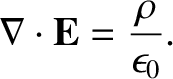 |
(2.492) |
[See Equation (2.466).]
Because
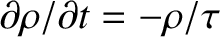 , it can be seen, from a comparison
of Equations (2.489) and (2.492), that
, it can be seen, from a comparison
of Equations (2.489) and (2.492), that
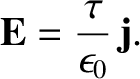 |
(2.493) |
However, the displacement current density is given by
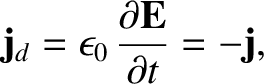 |
(2.494) |
because
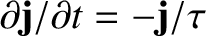 . Hence, we conclude that
the displacement current density cancels out the true current density, so that
. Hence, we conclude that
the displacement current density cancels out the true current density, so that
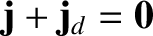 . This is just as well, because
. This is just as well, because
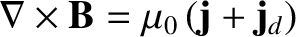 . [See Equation (2.479).] But, if
. [See Equation (2.479).] But, if
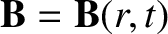 then, by symmetry,
then, by symmetry,
 has no radial component. [See Equation (A.174).] Thus, if the
current and displacement current are constrained, by symmetry, to be radial,
then they must sum to zero, otherwise the fourth Maxwell equation cannot be
satisfied. In fact, no magnetic field is generated in this particular example.
has no radial component. [See Equation (A.174).] Thus, if the
current and displacement current are constrained, by symmetry, to be radial,
then they must sum to zero, otherwise the fourth Maxwell equation cannot be
satisfied. In fact, no magnetic field is generated in this particular example.

 is a spherical polar coordinate (see Section A.23),
is a spherical polar coordinate (see Section A.23), 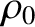 is a constant, and
is a constant, and 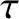 and
and 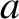 are positive constants.
Now, according to charge conservation,
[See Equation (2.473).]
By symmetry, we expect
are positive constants.
Now, according to charge conservation,
[See Equation (2.473).]
By symmetry, we expect
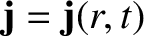 . Hence, it follows that
. Hence, it follows that
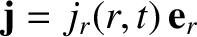 [because only a radial current has a non-zero
divergence when
[because only a radial current has a non-zero
divergence when
 ]. [See Equation (A.173).] Thus, the previous two equations
yield.
]. [See Equation (A.173).] Thus, the previous two equations
yield.
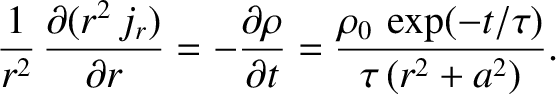
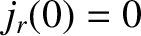 , to give
, to give
![$\displaystyle j_r(r) = \frac{\rho_0}{\tau}\,{\rm e}^{-t/\tau}\left[\frac{r-a\,\tan^{-1}(r/a)}{r^2}\right].$](img2078.png)
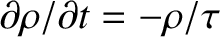 , it can be seen, from a comparison
of Equations (2.489) and (2.492), that
, it can be seen, from a comparison
of Equations (2.489) and (2.492), that
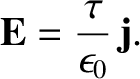
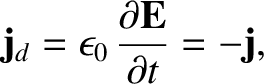
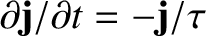 . Hence, we conclude that
the displacement current density cancels out the true current density, so that
. Hence, we conclude that
the displacement current density cancels out the true current density, so that
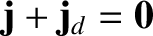 . This is just as well, because
. This is just as well, because
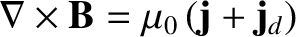 . [See Equation (2.479).] But, if
. [See Equation (2.479).] But, if
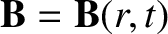 then, by symmetry,
then, by symmetry,
 has no radial component. [See Equation (A.174).] Thus, if the
current and displacement current are constrained, by symmetry, to be radial,
then they must sum to zero, otherwise the fourth Maxwell equation cannot be
satisfied. In fact, no magnetic field is generated in this particular example.
has no radial component. [See Equation (A.174).] Thus, if the
current and displacement current are constrained, by symmetry, to be radial,
then they must sum to zero, otherwise the fourth Maxwell equation cannot be
satisfied. In fact, no magnetic field is generated in this particular example.