Ideal Conductors

Most electrical conductors obey Ohm's law, and are termed ohmic conductors. Suppose that we apply an electric field to an ohmic conductor of very low resistivity. What is going to happen? According to Equation (2.117), the electric field drives very large currents inside the conductor. These currents will redistribute the electric charge within the conductor until the original electric field is canceled out. At this point, the currents stop flowing. It might be objected that the currents could keep flowing in closed loops. 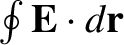According to Ohm's law, this would require a non-zero electromotive force (emf), $\oint {\bf E} \cdot d{\bf r}$ , acting around each loop (unless the conductor is a superconductor, with 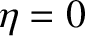$\eta = 0$ ). However, we know that in a steady state

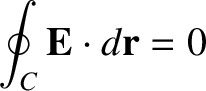$\displaystyle \oint_C {\bf E}\cdot d{\bf r} = 0$

(2.123)

around any closed loop . [See Equation (2.24).] This proves that a steady-state emf acting around a closed loop inside a conductor is impossible. The only other alternative is

$\displaystyle {\bf j} = {\bf E} = {\bf0}$

(2.124)

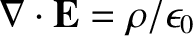everywhere inside the conductor. It immediately follows from the field equation $\nabla\cdot {\bf E} = \rho/\epsilon_0$ [see Equation (2.54)] that

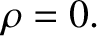$\displaystyle \rho = 0.$

(2.125)

We conclude that there is zero net electric charge in the interior of an ideal conductor. But, how can a conductor cancel out an applied electric field if it contains no internal electric charge? The answer is that the requisite charges reside on the surface of the conductor. (In reality, the charges lie within one or two atomic layers of the surface.)

Now, the difference in scalar potential between two points and 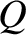is simply

$\displaystyle \phi(Q) - \phi(P) = \int_P^Q \nabla\phi \cdot d{\bf r} = - \int_P^Q {\bf E} \cdot d{\bf r}.$

(2.126)

[See Equation (2.17) and Section A.18.] However, if points and 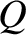both lie inside the same conductor then it is clear from Equations (2.124) and (2.126) that the potential difference between and 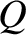is zero. This is true no matter where and 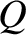are situated inside the conductor, so we conclude that the scalar potential must be uniform inside a conductor. One corollary of this fact is that the surface of a conductor is an equipotential (i.e., $\phi =$ constant) surface.

We have demonstrated that the electric field inside a conductor is zero. We can also demonstrate that the field within an empty cavity lying inside a conductor is zero, provided that there are no charges within the cavity. Let be the cavity in question, and let be its bounding surface. Because there are no electric charges within the cavity, the electric potential, $\phi$ , inside the cavity satisfies

$\displaystyle \nabla^2\phi = 0.$

(2.127)

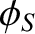[See Equation (2.99).] However, because corresponds to the inner surface of the conductor that surrounds the cavity, is an equipotential surface. In other words, the electric potential on takes a constant value, $\phi_S$ (say). So, we need to solve a simplified version of Poisson's equation, (2.127), throughout , subject to the boundary condition that $\phi=\phi_S$ on . One obvious solution to this problem is $\phi=\phi_S$ throughout and on . However, we showed in Section 2.1.10 that the solutions to Poisson's equation in a volume surrounded by a surface on which the potential is specified are unique. Thus, $\phi=\phi_S$ throughout and on is the only solution to the problem. 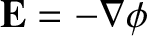It follows that the electric field ${\bf E} = -\nabla\phi$ is zero throughout the cavity. [See Equation (2.17).]

We have shown that if a charge-free cavity is completely enclosed by a conductor then no stationary distribution of charges outside the conductor can ever produce any electric fields inside the cavity. It follows that we can shield a sensitive piece of electrical equipment from stray external electric fields by placing it inside a metal can. In fact, a wire mesh cage will do, as long as the mesh spacing is not too wide. Such a cage is known as a Faraday cage.

Consider a small region lying on the surface of a conductor. Suppose that the local surface electric charge density is 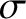$\sigma$ , and that the electric field just outside the conductor is ${\bf E}$ . Note that this field must be directed normal to the surface of the conductor. Any parallel component would be shorted out by surface currents. Another way of saying this is that the surface of a conductor is an equipotential. 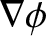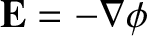We know that $\nabla\phi$ is always perpendicular to an equipotential (see Section A.18), so ${\bf E} = -\nabla\phi$ [see Equation (2.17)] must be locally perpendicular to a conducting surface. Let us use Gauss's law [see Equation (2.58)],

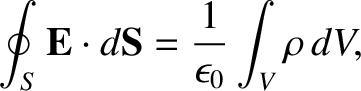$\displaystyle \oint_S {\bf E} \cdot d{\bf S} = \frac{1}{\epsilon_0} \int_V \rho \,dV,$

(2.128)

where the volume is a so-called Gaussian pill-box. See Figure 2.5. A Gaussian pill-box is a volume of space whose shape is similar to an old-fashioned pill-box (or a modern pizza box). Let the two flat ends of the pill-box be aligned parallel to the surface of the conductor, with the surface running between them, and let the comparatively short sides be perpendicular to the surface. It is clear that ${\bf E}$ is parallel to the sides of the box, so the sides make no contribution to the surface integral. The end of the box that lies inside the conductor also makes no contribution, because ${\bf E} ={\bf0}$ inside a conductor. Thus, the only non-zero contribution to the surface integral comes from the end lying in free space. 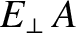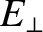This contribution is simply $E_\perp \,A$ , where $E_\perp$ denotes an outward pointing (from the conductor) normal electric field, and is the cross-sectional area of the box. 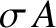The charge enclosed by the box is simply $\sigma\,A$ , from the definition of a surface charge density. Thus, Gauss's law yields

$\displaystyle E_\perp = \frac{\sigma}{\epsilon_0}$

(2.129)

as the relationship between the normal electric field immediately outside a conductor and the surface charge density.

**Figure 2.5:** The surface of a conductor.
$\includegraphics[height=2.5in]{Chapter03/fig5_2.eps}$

Let us look at the electric field generated by a sheet charge distribution a little more carefully. Suppose that the charge per unit area is 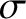$\sigma$ . By symmetry, we expect the field generated below the sheet to be the mirror image of that above the sheet (at least, locally). 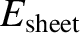Thus, if apply Gauss's law to a pill-box of cross-sectional area , as shown in Figure 2.6, then the two ends both contribute $E_{\rm sheet}\,A$ to the surface integral, where $E_{\rm sheet}$ is the normal electric field generated above and below the sheet. The charge enclosed by the pill-box is just 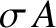$\sigma\,A$ . Thus, Gauss's law yields a symmetric electric field

$\begin{displaymath}E_{\rm sheet}= \left\{ \begin{array}{lll} +\sigma/(2\,\epsilo... ...epsilon_0)&\mbox{\hspace{2cm}}&\mbox{below} \end{array}\right..\end{displaymath}$

(2.130)

So, how do we get the asymmetric electric field of a conducting surface, which is zero immediately below the surface (i.e., inside the conductor) and non-zero immediately above it? Clearly, we have to add in an external field (i.e., a field that is not generated locally by the sheet charge). The requisite field is

$\displaystyle E_{\rm ext} = \frac{\sigma}{2\,\epsilon_0}$

(2.131)

both above and below the charge sheet. The total field is the sum of the field generated locally by the charge sheet and the external field. Thus, we obtain

$\begin{displaymath}E_{\rm total}= \left\{ \begin{array}{lll} +\sigma/\epsilon_0&... ... [0.5ex] 0&\mbox{\hspace{2cm}}&\mbox{below} \end{array}\right.,\end{displaymath}$

(2.132)

which is in agreement with Equation (2.129). Now, the external electric field exerts a force on the charge sheet. Of course, the field generated locally by the sheet itself cannot exert a local force (i.e., by Newton's third law of motion, the charge sheet cannot locally exert a force on itself; see Section 1.2.4). Thus, the force per unit area acting on the surface of a conductor always acts outward, and is given by

$\displaystyle p = \sigma \,E_{\rm ext} = \frac{\sigma^2}{2\,\epsilon_0}.$

(2.133)

[See Equation (2.10).] We conclude that there is an electrostatic pressure acting on any charged conductor. This effect can be observed by charging up soap bubbles; the additional electrostatic pressure eventually causes them to burst.

**Figure 2.6:** The electric field of a sheet charge.
$\includegraphics[height=2.25in]{Chapter03/fig5_3.eps}$

Making use of Equations (2.131) and (2.133), the electrostatic pressure acting at the surface of a conductor can also be written

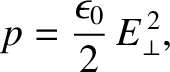$\displaystyle p = \frac{\epsilon_0}{2} \,E_\perp^{\,2},$

(2.134)

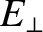where $E_\perp$ is the electric field-strength immediately above the surface of the conductor. Note that, according to the previous formula, the electrostatic pressure is equivalent to the energy density of the electric field immediately outside the conductor. [See Equation (2.84).] This is not a coincidence. Suppose that the conductor expands normally by an average distance 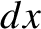, due to the electrostatic pressure. The electric field is excluded from the region into which the conductor expands. 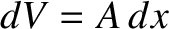The volume of this region is $dV = A \,dx$ , where is the surface area of the conductor. 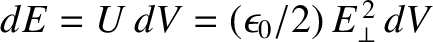Thus, the energy of the electric field decreases by an amount $dE = U\,dV = (\epsilon_0/2) \,E_\perp^{\,2} \,dV$ , where is the energy density of the field. This decrease in energy can be ascribed to the work that the field does on the conductor in order to make it expand. This work is $dW = p\,A\,dx$ , where is the force per unit area that the field exerts on the conductor. Thus, 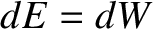, from energy conservation, giving

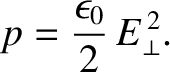$\displaystyle p = \frac{\epsilon_0}{2} \,E_\perp^{\,2}.$

(2.135)

Incidentally, this technique for calculating a force, given an expression for the energy of a system as a function of some adjustable parameter, is called the principle of virtual work.