Uniqueness Theorem
Consider a volume  bounded by some surface
bounded by some surface  . Suppose that we are given
the electric charge density
. Suppose that we are given
the electric charge density 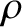 throughout
throughout  , and the (not necessarily constant) value of the scalar potential
, and the (not necessarily constant) value of the scalar potential
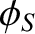 on
on  . Is this sufficient information for Poisson's equation to uniquely specify the scalar
potential throughout
. Is this sufficient information for Poisson's equation to uniquely specify the scalar
potential throughout  ? Suppose, for the sake of argument, that the
solution is not unique. Let there be two different potentials
? Suppose, for the sake of argument, that the
solution is not unique. Let there be two different potentials  and
and  that both
satisfy
throughout
that both
satisfy
throughout  , and
on
, and
on  . We can form the difference between these two potentials:
. We can form the difference between these two potentials:
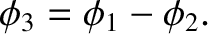 |
(2.104) |
The potential  clearly satisfies
clearly satisfies
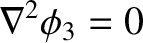 |
(2.105) |
throughout  , and
, and
 |
(2.106) |
on  .
.
Now,
 |
(2.107) |
(See Section A.24.)
Thus, making use of the divergence theorem,
![$\displaystyle \int_V \left[ (\nabla\phi_3)^2 +\phi_3 \nabla^2\phi_3\right] dV =
\oint_S \phi_3 \nabla \phi_3\cdot d{\bf S}.$](img1303.png) |
(2.108) |
(See Section A.20.)
But,
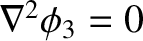 throughout
throughout  , and
, and 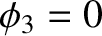 on
on  , so the
previous equation reduces
to
, so the
previous equation reduces
to
 |
(2.109) |
Note that
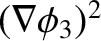 is a positive definite quantity. The only way in
which the volume integral of a positive definite quantity can be zero is if
that quantity itself is zero throughout the volume. This is not necessarily the
case for a non-positive definite quantity, because we could have positive and negative
contributions from various regions inside the volume that cancel one another out.
Thus, because
is a positive definite quantity. The only way in
which the volume integral of a positive definite quantity can be zero is if
that quantity itself is zero throughout the volume. This is not necessarily the
case for a non-positive definite quantity, because we could have positive and negative
contributions from various regions inside the volume that cancel one another out.
Thus, because
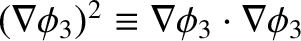 is positive definite, it is zero throughout
is positive definite, it is zero throughout  . It follows that
. It follows that
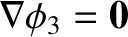 throughout
throughout  ,
and, hence, that
,
and, hence, that
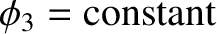 |
(2.110) |
throughout  . However, we know that
. However, we know that 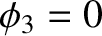 on
on  , so we get
, so we get
 |
(2.111) |
throughout  . In other words,
. In other words,
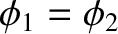 |
(2.112) |
throughout  and on
and on  . Our initial supposition that
. Our initial supposition that  and
and  are two different solutions of Poisson's equation, satisfying the same
boundary conditions, turns out to be incorrect. Hence, we deduce that the solutions to Poisson's equation in a
volume bounded by a surface on which the electric potential is specified are unique. This important
result is known as the uniqueness theorem.
are two different solutions of Poisson's equation, satisfying the same
boundary conditions, turns out to be incorrect. Hence, we deduce that the solutions to Poisson's equation in a
volume bounded by a surface on which the electric potential is specified are unique. This important
result is known as the uniqueness theorem.
 bounded by some surface
bounded by some surface  . Suppose that we are given
the electric charge density
. Suppose that we are given
the electric charge density 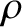 throughout
throughout  , and the (not necessarily constant) value of the scalar potential
, and the (not necessarily constant) value of the scalar potential
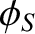 on
on  . Is this sufficient information for Poisson's equation to uniquely specify the scalar
potential throughout
. Is this sufficient information for Poisson's equation to uniquely specify the scalar
potential throughout  ? Suppose, for the sake of argument, that the
solution is not unique. Let there be two different potentials
? Suppose, for the sake of argument, that the
solution is not unique. Let there be two different potentials  and
and  that both
satisfy
that both
satisfy
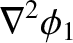
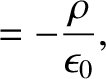
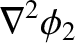

 , and
, and
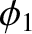

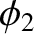
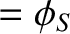
 . We can form the difference between these two potentials:
. We can form the difference between these two potentials:
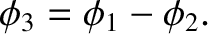
 clearly satisfies
clearly satisfies
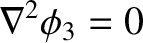
 , and
, and

 .
.

![$\displaystyle \int_V \left[ (\nabla\phi_3)^2 +\phi_3 \nabla^2\phi_3\right] dV =
\oint_S \phi_3 \nabla \phi_3\cdot d{\bf S}.$](img1303.png)
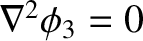 throughout
throughout  , and
, and 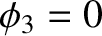 on
on  , so the
previous equation reduces
to
, so the
previous equation reduces
to

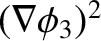 is a positive definite quantity. The only way in
which the volume integral of a positive definite quantity can be zero is if
that quantity itself is zero throughout the volume. This is not necessarily the
case for a non-positive definite quantity, because we could have positive and negative
contributions from various regions inside the volume that cancel one another out.
Thus, because
is a positive definite quantity. The only way in
which the volume integral of a positive definite quantity can be zero is if
that quantity itself is zero throughout the volume. This is not necessarily the
case for a non-positive definite quantity, because we could have positive and negative
contributions from various regions inside the volume that cancel one another out.
Thus, because
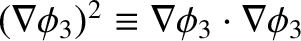 is positive definite, it is zero throughout
is positive definite, it is zero throughout  . It follows that
. It follows that
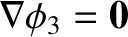 throughout
throughout  ,
and, hence, that
,
and, hence, that
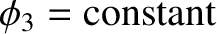
 . However, we know that
. However, we know that 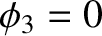 on
on  , so we get
, so we get

 . In other words,
. In other words,
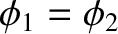
 and on
and on  . Our initial supposition that
. Our initial supposition that  and
and  are two different solutions of Poisson's equation, satisfying the same
boundary conditions, turns out to be incorrect. Hence, we deduce that the solutions to Poisson's equation in a
volume bounded by a surface on which the electric potential is specified are unique. This important
result is known as the uniqueness theorem.
are two different solutions of Poisson's equation, satisfying the same
boundary conditions, turns out to be incorrect. Hence, we deduce that the solutions to Poisson's equation in a
volume bounded by a surface on which the electric potential is specified are unique. This important
result is known as the uniqueness theorem.