Next: About this document ... Up: Vector Algebra and Vector Previous: Curvilinear Coordinates
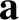 ,
, 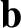 ,
, 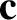 ,
, 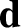 are general vectors;
are general vectors; 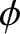 ,
, 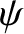 are general scalar fields;
are general scalar fields; 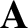 ,
, 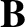 are general vector fields;
are general vector fields;
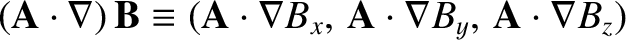 and
and
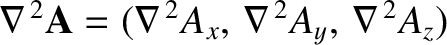 (but, only in Cartesian coordinates)
(but, only in Cartesian coordinates)
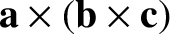 |
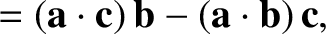 |
(1.176) |
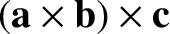 |
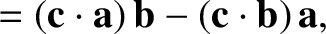 |
(1.177) |
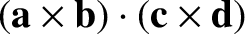 |
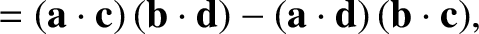 |
(1.178) |
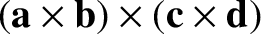 |
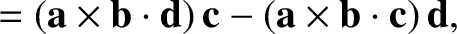 |
(1.179) |
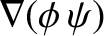 |
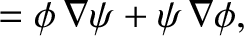 |
(1.180) |
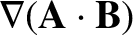 |
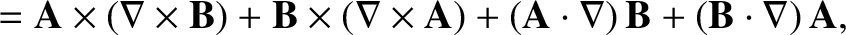 |
(1.181) |
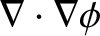 |
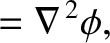 |
(1.182) |
 |
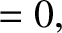 |
(1.183) |
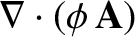 |
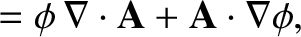 |
(1.184) |
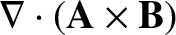 |
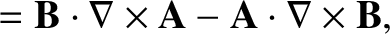 |
(1.185) |
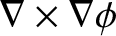 |
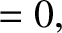 |
(1.186) |
 |
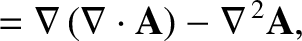 |
(1.187) |
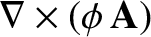 |
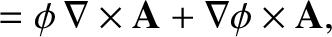 |
(1.188) |
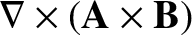 |
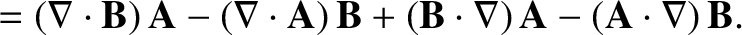 |
(1.189) |