Ohm's Law
A conductor is a medium that contains free electric charges (usually electrons) that acquire a net drift velocity in the presence of an applied electric field, giving rise to an
electric current flowing in the same direction as the field. The well-known
relationship between the current and the voltage in a typical conductor is given by
Ohm's law:
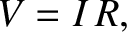 |
(2.113) |
where  is the voltage drop across a conductor of electrical resistance
is the voltage drop across a conductor of electrical resistance  through which a current
through which a current  flows. Incidentally, the unit of electric current is the ampere (or amp) (A), which is equivalent to a coulomb per second.
Furthermore, the unit of electrical resistance is the
ohm (
flows. Incidentally, the unit of electric current is the ampere (or amp) (A), which is equivalent to a coulomb per second.
Furthermore, the unit of electrical resistance is the
ohm ( ), which is equivalent to a volt per ampere.
), which is equivalent to a volt per ampere.
Let us generalize Ohm's law so that it is expressed in terms
of the electric field,  , and current density,
, and current density, 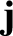 , at a given point inside the conductor, rather than the global quantities
, at a given point inside the conductor, rather than the global quantities  and
and  .
Here, the magnitude of the current density vector,
.
Here, the magnitude of the current density vector, 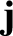 , measures the amount of current flowing per unit time
per unit cross-sectional area, whereas the direction of the vector specifies the direction of the current flow.
Consider a length
, measures the amount of current flowing per unit time
per unit cross-sectional area, whereas the direction of the vector specifies the direction of the current flow.
Consider a length
 of a conductor of uniform cross-sectional area
of a conductor of uniform cross-sectional area  through which a net electric current
through which a net electric current
 flows. In general, we expect the electrical
resistance of the conductor to be proportional to its length,
flows. In general, we expect the electrical
resistance of the conductor to be proportional to its length,  , and inversely
proportional to its cross-sectional area,
, and inversely
proportional to its cross-sectional area,  (i.e., we expect it to be harder to push an electrical
current down a long
rather than a short wire, and easier to push an electrical current down a wide rather
than a narrow conducting channel.) Thus, we can write
(i.e., we expect it to be harder to push an electrical
current down a long
rather than a short wire, and easier to push an electrical current down a wide rather
than a narrow conducting channel.) Thus, we can write
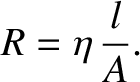 |
(2.114) |
Here, the constant 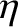 is called the resistivity of the conducting medium, and is measured in
units of ohm-meters. Hence, Ohm's law becomes
is called the resistivity of the conducting medium, and is measured in
units of ohm-meters. Hence, Ohm's law becomes
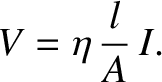 |
(2.115) |
However, 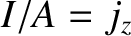 (supposing that the conductor is aligned along the
(supposing that the conductor is aligned along the  -axis)
and
-axis)
and 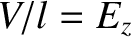 [see Equation (2.17)], so the previous equation reduces to
[see Equation (2.17)], so the previous equation reduces to
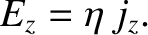 |
(2.116) |
Because there is nothing special about the  -axis (in an isotropic conducting medium), the
previous formula immediately generalizes to
-axis (in an isotropic conducting medium), the
previous formula immediately generalizes to
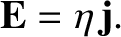 |
(2.117) |
This is the most fundamental form of Ohm's law.
It is fairly easy to account for the previous equation at the microscopic level. Consider a metal
that has 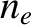 free electrons per unit volume. Of course, the metal also
has a fixed lattice of metal ions whose charge per unit volume is equal and
opposite to that of the free electrons, rendering the medium electrically neutral.
In the presence of an electric field
free electrons per unit volume. Of course, the metal also
has a fixed lattice of metal ions whose charge per unit volume is equal and
opposite to that of the free electrons, rendering the medium electrically neutral.
In the presence of an electric field  , a given free electron is subject to an electrical force
, a given free electron is subject to an electrical force
 [see Equation (2.10)], and therefore accelerates
(from rest at
[see Equation (2.10)], and therefore accelerates
(from rest at  ) such that its drift velocity is written
) such that its drift velocity is written
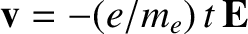 ,
where
,
where  is the electron charge, and
is the electron charge, and 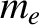 the electron mass. Suppose
that, on average, a drifting electron collides with a metal ion once every
the electron mass. Suppose
that, on average, a drifting electron collides with a metal ion once every 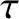 seconds. Given that a metal ion is much more massive than an electron,
we expect a free electron to lose all of the momentum it had previously acquired from
the electric field during such a collision.
It follows that the mean drift velocity of the free electrons is
seconds. Given that a metal ion is much more massive than an electron,
we expect a free electron to lose all of the momentum it had previously acquired from
the electric field during such a collision.
It follows that the mean drift velocity of the free electrons is
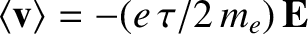 . Hence, the mean current density
is
. Hence, the mean current density
is
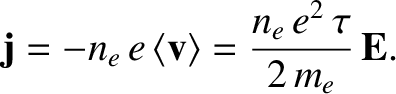 |
(2.118) |
Thus, we can account for Equation (2.117),
as long as the resistivity takes the form
 |
(2.119) |
We conclude that the resistivity of a typical conducting medium is determined
by the number density of free electrons, as well as the mean collision
rate of these electrons with the fixed ions.
A free charge  that moves through a voltage drop
that moves through a voltage drop  acquires an energy
acquires an energy 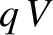 from the
electric field. (See Section 2.1.5.) In a conducting medium, this energy is dissipated as heat (the conversion to heat takes place each time a free charge collides with a fixed ion). This particular type of heating
is called ohmic heating or Joule heating. Suppose that
from the
electric field. (See Section 2.1.5.) In a conducting medium, this energy is dissipated as heat (the conversion to heat takes place each time a free charge collides with a fixed ion). This particular type of heating
is called ohmic heating or Joule heating. Suppose that  charges per unit time pass through a
conductor. The current flowing through the conductor is obviously
charges per unit time pass through a
conductor. The current flowing through the conductor is obviously 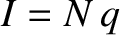 . The total energy gained by the
charges, which appears as heat inside the conductor, is
. The total energy gained by the
charges, which appears as heat inside the conductor, is
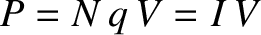 |
(2.120) |
per unit time. Thus, the heating power is
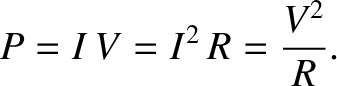 |
(2.121) |
Equations (2.120) and (2.121) generalize to
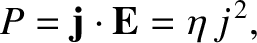 |
(2.122) |
where  is now the power dissipated per unit volume inside the conducting medium.
is now the power dissipated per unit volume inside the conducting medium.
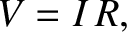
 is the voltage drop across a conductor of electrical resistance
is the voltage drop across a conductor of electrical resistance  through which a current
through which a current  flows. Incidentally, the unit of electric current is the ampere (or amp) (A), which is equivalent to a coulomb per second.
Furthermore, the unit of electrical resistance is the
ohm (
flows. Incidentally, the unit of electric current is the ampere (or amp) (A), which is equivalent to a coulomb per second.
Furthermore, the unit of electrical resistance is the
ohm ( ), which is equivalent to a volt per ampere.
), which is equivalent to a volt per ampere.
 , and current density,
, and current density, 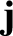 , at a given point inside the conductor, rather than the global quantities
, at a given point inside the conductor, rather than the global quantities  and
and  .
Here, the magnitude of the current density vector,
.
Here, the magnitude of the current density vector, 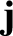 , measures the amount of current flowing per unit time
per unit cross-sectional area, whereas the direction of the vector specifies the direction of the current flow.
Consider a length
, measures the amount of current flowing per unit time
per unit cross-sectional area, whereas the direction of the vector specifies the direction of the current flow.
Consider a length
 of a conductor of uniform cross-sectional area
of a conductor of uniform cross-sectional area  through which a net electric current
through which a net electric current
 flows. In general, we expect the electrical
resistance of the conductor to be proportional to its length,
flows. In general, we expect the electrical
resistance of the conductor to be proportional to its length,  , and inversely
proportional to its cross-sectional area,
, and inversely
proportional to its cross-sectional area,  (i.e., we expect it to be harder to push an electrical
current down a long
rather than a short wire, and easier to push an electrical current down a wide rather
than a narrow conducting channel.) Thus, we can write
(i.e., we expect it to be harder to push an electrical
current down a long
rather than a short wire, and easier to push an electrical current down a wide rather
than a narrow conducting channel.) Thus, we can write
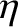 is called the resistivity of the conducting medium, and is measured in
units of ohm-meters. Hence, Ohm's law becomes
is called the resistivity of the conducting medium, and is measured in
units of ohm-meters. Hence, Ohm's law becomes
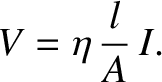
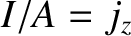 (supposing that the conductor is aligned along the
(supposing that the conductor is aligned along the  -axis)
and
-axis)
and 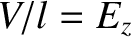 [see Equation (2.17)], so the previous equation reduces to
[see Equation (2.17)], so the previous equation reduces to
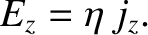
 -axis (in an isotropic conducting medium), the
previous formula immediately generalizes to
This is the most fundamental form of Ohm's law.
-axis (in an isotropic conducting medium), the
previous formula immediately generalizes to
This is the most fundamental form of Ohm's law.
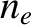 free electrons per unit volume. Of course, the metal also
has a fixed lattice of metal ions whose charge per unit volume is equal and
opposite to that of the free electrons, rendering the medium electrically neutral.
In the presence of an electric field
free electrons per unit volume. Of course, the metal also
has a fixed lattice of metal ions whose charge per unit volume is equal and
opposite to that of the free electrons, rendering the medium electrically neutral.
In the presence of an electric field  , a given free electron is subject to an electrical force
, a given free electron is subject to an electrical force
 [see Equation (2.10)], and therefore accelerates
(from rest at
[see Equation (2.10)], and therefore accelerates
(from rest at  ) such that its drift velocity is written
) such that its drift velocity is written
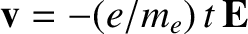 ,
where
,
where  is the electron charge, and
is the electron charge, and 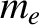 the electron mass. Suppose
that, on average, a drifting electron collides with a metal ion once every
the electron mass. Suppose
that, on average, a drifting electron collides with a metal ion once every 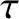 seconds. Given that a metal ion is much more massive than an electron,
we expect a free electron to lose all of the momentum it had previously acquired from
the electric field during such a collision.
It follows that the mean drift velocity of the free electrons is
seconds. Given that a metal ion is much more massive than an electron,
we expect a free electron to lose all of the momentum it had previously acquired from
the electric field during such a collision.
It follows that the mean drift velocity of the free electrons is
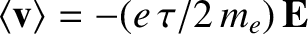 . Hence, the mean current density
is
. Hence, the mean current density
is
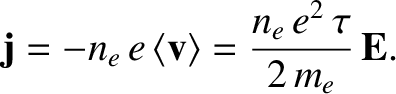

 that moves through a voltage drop
that moves through a voltage drop  acquires an energy
acquires an energy 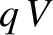 from the
electric field. (See Section 2.1.5.) In a conducting medium, this energy is dissipated as heat (the conversion to heat takes place each time a free charge collides with a fixed ion). This particular type of heating
is called ohmic heating or Joule heating. Suppose that
from the
electric field. (See Section 2.1.5.) In a conducting medium, this energy is dissipated as heat (the conversion to heat takes place each time a free charge collides with a fixed ion). This particular type of heating
is called ohmic heating or Joule heating. Suppose that  charges per unit time pass through a
conductor. The current flowing through the conductor is obviously
charges per unit time pass through a
conductor. The current flowing through the conductor is obviously 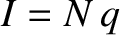 . The total energy gained by the
charges, which appears as heat inside the conductor, is
. The total energy gained by the
charges, which appears as heat inside the conductor, is
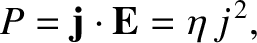
 is now the power dissipated per unit volume inside the conducting medium.
is now the power dissipated per unit volume inside the conducting medium.