Next: Magnetic Induction Up: Magnetostatic Fields Previous: Ampère's Circuital Law
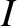 .
The winding is sufficiently tight that each turn of the solenoid is well
approximated as
a circular wire loop, lying in the plane perpendicular to the axis of
the solenoid, that carries a current
.
The winding is sufficiently tight that each turn of the solenoid is well
approximated as
a circular wire loop, lying in the plane perpendicular to the axis of
the solenoid, that carries a current 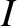 . Suppose that there
are
. Suppose that there
are 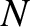 such turns per unit axial length of the solenoid. What is the
magnitude of the magnetic field in the core of the solenoid?
such turns per unit axial length of the solenoid. What is the
magnitude of the magnetic field in the core of the solenoid?
In order to answer this question, let us apply Ampère's circuital
law to the rectangular loop  . We must first find the line integral
of the magnetic field around
. We must first find the line integral
of the magnetic field around 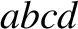 . Along
. Along 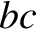 and
and 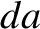 the magnetic field
is essentially perpendicular to the loop, so there is no contribution to
the line integral from these sections of the loop.
Along
the magnetic field
is essentially perpendicular to the loop, so there is no contribution to
the line integral from these sections of the loop.
Along 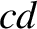 the magnetic field is approximately uniform,
of magnitude
the magnetic field is approximately uniform,
of magnitude 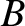 , say, and is directed parallel to the loop. Thus, the
contribution to the line integral from this section of the loop
is
, say, and is directed parallel to the loop. Thus, the
contribution to the line integral from this section of the loop
is 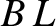 , where
, where 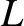 is the length of
is the length of 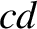 .
Along
.
Along 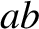 the magnetic field-strength is essentially negligible, so
this section of the loop makes no contribution to the line
integral. It follows that the line integral of the
magnetic field around
the magnetic field-strength is essentially negligible, so
this section of the loop makes no contribution to the line
integral. It follows that the line integral of the
magnetic field around 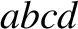 is simply
is simply
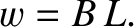 |
(2.277) |
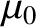 multiplied by the algebraic sum of
the currents that pass through the plane of the loop
multiplied by the algebraic sum of
the currents that pass through the plane of the loop 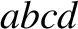 . Because the length of the
loop along the axis of the solenoid is
. Because the length of the
loop along the axis of the solenoid is 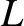 , the loop encloses
, the loop encloses 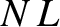 turns of the solenoid, each of which carries a current
turns of the solenoid, each of which carries a current 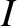 . Thus, the total
current that passes through the plane of the loop is
. Thus, the total
current that passes through the plane of the loop is 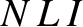 . This current counts as
a positive current, because if we look against the direction of the
currents flowing in each turn
(i.e., into the page in the figure) then the loop
. This current counts as
a positive current, because if we look against the direction of the
currents flowing in each turn
(i.e., into the page in the figure) then the loop 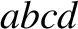 circulates
these currents in a counter-clockwise direction. Ampère's circuital law yields
circulates
these currents in a counter-clockwise direction. Ampère's circuital law yields
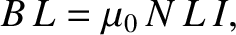 |
(2.278) |