Ampère's Circuital Law
According to Equation (2.251),
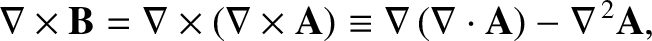 |
(2.266) |
where use has been made of Equation (A.187). However, Equation (2.262) indicates
that
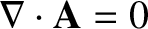 for a steady current distribution. Hence, the previous equation simplifies to give
for a steady current distribution. Hence, the previous equation simplifies to give
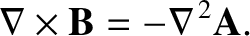 |
(2.267) |
The previous equation can be combined with Equation (2.252) to give
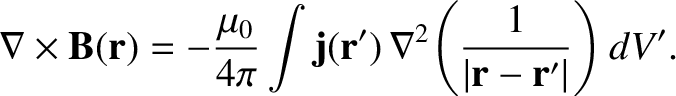 |
(2.268) |
However, according to Equation (2.56),
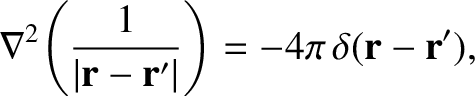 |
(2.269) |
so we obtain
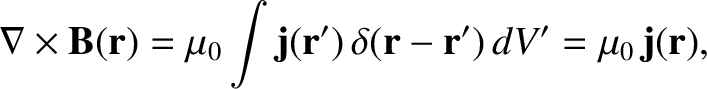 |
(2.270) |
where use has been made of Equation (2.47).
The previous equation can be written
 |
(2.271) |
Let us calculate the flux of
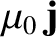 through some surface
through some surface  , bounded by a loop
, bounded by a loop  . Making
use of the previous field equation, as well as the curl theorem (see Section A.22), we obtain
. Making
use of the previous field equation, as well as the curl theorem (see Section A.22), we obtain
 |
(2.272) |
In other words, the line integral of the magnetic field around some loop  is equal to
is equal to 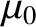 multiplied by the
net electric current flowing across some surface,
multiplied by the
net electric current flowing across some surface,  , attached to the loop. This result is known as Ampère's circuital law. Note that because the current density associated with a steady current pattern is divergence free [see Equation (2.261)], the net current flowing across any surface attached to
, attached to the loop. This result is known as Ampère's circuital law. Note that because the current density associated with a steady current pattern is divergence free [see Equation (2.261)], the net current flowing across any surface attached to  is the same. (See Section A.20.)
Of course, when performing the line integral we have to choose an arbitrary sense of
circulation around the loop. Once we have done this, any currents
that the loop circles in an counter-clockwise direction (looking
against the direction of the current) count as positive currents, whereas any currents
that the loop circles in a clockwise direction (looking
against the direction of the current) count as negative currents.
is the same. (See Section A.20.)
Of course, when performing the line integral we have to choose an arbitrary sense of
circulation around the loop. Once we have done this, any currents
that the loop circles in an counter-clockwise direction (looking
against the direction of the current) count as positive currents, whereas any currents
that the loop circles in a clockwise direction (looking
against the direction of the current) count as negative currents.
Let us apply Ampère's circuital law to the trivial case of a circular loop of radius  that lies in the plane
perpendicular to a long straight wire, carrying a current
that lies in the plane
perpendicular to a long straight wire, carrying a current  , that passes though its center. By symmetry, we expect the magnetic field to be of the form
, that passes though its center. By symmetry, we expect the magnetic field to be of the form
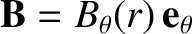 , where
, where  ,
,  ,
,  are right-handed cylindrical polar
coordinates defined such that the wire runs along the
are right-handed cylindrical polar
coordinates defined such that the wire runs along the  -axis. (See Section A.23.)
If the chosen sense of circulation around the loop is in the direction of increasing
-axis. (See Section A.23.)
If the chosen sense of circulation around the loop is in the direction of increasing  then
then  counts as a positive
current.
Thus, Equation (2.272) yields
counts as a positive
current.
Thus, Equation (2.272) yields
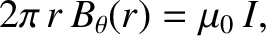 |
(2.273) |
or
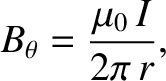 |
(2.274) |
which is equivalent to Equation (2.206).
Figure 2.23:
An example use of Ampère's circuital law.
|
|
As another example of the use of Ampère's circuital law, let us calculate the magnetic field
generated by a cylindrical current annulus of inner radius 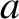 ,
and outer radius
,
and outer radius 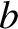 , co-axial with the
, co-axial with the  -axis, and carrying a uniformly
distributed
-axis, and carrying a uniformly
distributed  -directed current
-directed current  . By symmetry, and also by analogy
with the magnetic field generated by a straight wire, we expect the current distribution to generate a
magnetic field of the form
. By symmetry, and also by analogy
with the magnetic field generated by a straight wire, we expect the current distribution to generate a
magnetic field of the form
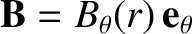 , where
, where  ,
,  ,
,  are right-handed cylindrical polar coordinates. (See Section A.23.)
Let us apply Ampère's circuital law to an imaginary circular loop in the
are right-handed cylindrical polar coordinates. (See Section A.23.)
Let us apply Ampère's circuital law to an imaginary circular loop in the  -
- plane, of radius
plane, of radius
 , centered on the
, centered on the  -axis. See Figure 2.23. Such a loop is generally known as an Ampèrian loop.
As before, if the chosen sense of circulation around the loop is in the direction of increasing
-axis. See Figure 2.23. Such a loop is generally known as an Ampèrian loop.
As before, if the chosen sense of circulation around the loop is in the direction of increasing  then
then  counts as a positive
current. According to
Ampère's circuital law, the line integral of the magnetic field around the loop is equal to
the current passing through the plane of the loop, multiplied by
counts as a positive
current. According to
Ampère's circuital law, the line integral of the magnetic field around the loop is equal to
the current passing through the plane of the loop, multiplied by 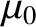 . The line integral is easy to calculate because the magnetic field is everywhere tangential to the
loop. We obtain
. The line integral is easy to calculate because the magnetic field is everywhere tangential to the
loop. We obtain
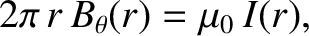
where 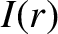 is the current that passes through an Ampèrian loop of radius
is the current that passes through an Ampèrian loop of radius  .
Simple arguments involving proportion reveal that
.
Simple arguments involving proportion reveal that
![\begin{displaymath}I(r) = \left\{
\begin{array}{lcl}
0&\mbox{\hspace{1cm}}&r<a\\...
...2)\right] I&&a\leq r\leq b\\ [0.5ex]
I&&b<r
\end{array}\right..\end{displaymath}](img1658.png) |
(2.275) |
Hence,
![\begin{displaymath}B_\theta(r) = \left\{
\begin{array}{lcl}
0&\mbox{\hspace{1cm}...
...q r\leq b\\ [0.5ex]
\mu_0\,I/(2\pi\,r)&&b<r
\end{array}\right..\end{displaymath}](img1659.png) |
(2.276) |
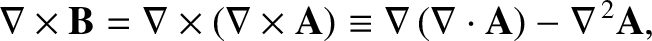
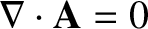 for a steady current distribution. Hence, the previous equation simplifies to give
for a steady current distribution. Hence, the previous equation simplifies to give
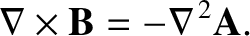
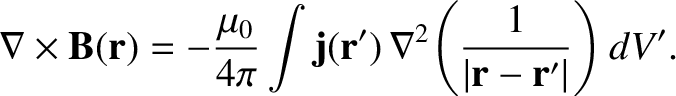
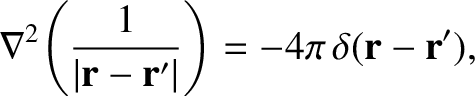
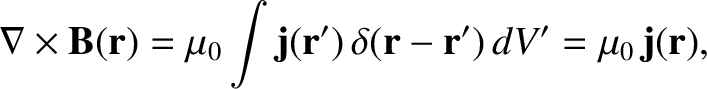
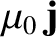 through some surface
through some surface  , bounded by a loop
, bounded by a loop  . Making
use of the previous field equation, as well as the curl theorem (see Section A.22), we obtain
In other words, the line integral of the magnetic field around some loop
. Making
use of the previous field equation, as well as the curl theorem (see Section A.22), we obtain
In other words, the line integral of the magnetic field around some loop  is equal to
is equal to 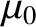 multiplied by the
net electric current flowing across some surface,
multiplied by the
net electric current flowing across some surface,  , attached to the loop. This result is known as Ampère's circuital law. Note that because the current density associated with a steady current pattern is divergence free [see Equation (2.261)], the net current flowing across any surface attached to
, attached to the loop. This result is known as Ampère's circuital law. Note that because the current density associated with a steady current pattern is divergence free [see Equation (2.261)], the net current flowing across any surface attached to  is the same. (See Section A.20.)
Of course, when performing the line integral we have to choose an arbitrary sense of
circulation around the loop. Once we have done this, any currents
that the loop circles in an counter-clockwise direction (looking
against the direction of the current) count as positive currents, whereas any currents
that the loop circles in a clockwise direction (looking
against the direction of the current) count as negative currents.
is the same. (See Section A.20.)
Of course, when performing the line integral we have to choose an arbitrary sense of
circulation around the loop. Once we have done this, any currents
that the loop circles in an counter-clockwise direction (looking
against the direction of the current) count as positive currents, whereas any currents
that the loop circles in a clockwise direction (looking
against the direction of the current) count as negative currents.
 that lies in the plane
perpendicular to a long straight wire, carrying a current
that lies in the plane
perpendicular to a long straight wire, carrying a current  , that passes though its center. By symmetry, we expect the magnetic field to be of the form
, that passes though its center. By symmetry, we expect the magnetic field to be of the form
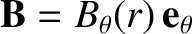 , where
, where  ,
,  ,
,  are right-handed cylindrical polar
coordinates defined such that the wire runs along the
are right-handed cylindrical polar
coordinates defined such that the wire runs along the  -axis. (See Section A.23.)
If the chosen sense of circulation around the loop is in the direction of increasing
-axis. (See Section A.23.)
If the chosen sense of circulation around the loop is in the direction of increasing  then
then  counts as a positive
current.
Thus, Equation (2.272) yields
counts as a positive
current.
Thus, Equation (2.272) yields
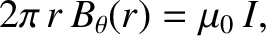
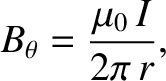
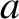 ,
and outer radius
,
and outer radius 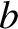 , co-axial with the
, co-axial with the  -axis, and carrying a uniformly
distributed
-axis, and carrying a uniformly
distributed  -directed current
-directed current  . By symmetry, and also by analogy
with the magnetic field generated by a straight wire, we expect the current distribution to generate a
magnetic field of the form
. By symmetry, and also by analogy
with the magnetic field generated by a straight wire, we expect the current distribution to generate a
magnetic field of the form
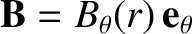 , where
, where  ,
,  ,
,  are right-handed cylindrical polar coordinates. (See Section A.23.)
Let us apply Ampère's circuital law to an imaginary circular loop in the
are right-handed cylindrical polar coordinates. (See Section A.23.)
Let us apply Ampère's circuital law to an imaginary circular loop in the  -
- plane, of radius
plane, of radius
 , centered on the
, centered on the  -axis. See Figure 2.23. Such a loop is generally known as an Ampèrian loop.
As before, if the chosen sense of circulation around the loop is in the direction of increasing
-axis. See Figure 2.23. Such a loop is generally known as an Ampèrian loop.
As before, if the chosen sense of circulation around the loop is in the direction of increasing  then
then  counts as a positive
current. According to
Ampère's circuital law, the line integral of the magnetic field around the loop is equal to
the current passing through the plane of the loop, multiplied by
counts as a positive
current. According to
Ampère's circuital law, the line integral of the magnetic field around the loop is equal to
the current passing through the plane of the loop, multiplied by 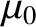 . The line integral is easy to calculate because the magnetic field is everywhere tangential to the
loop. We obtain
. The line integral is easy to calculate because the magnetic field is everywhere tangential to the
loop. We obtain
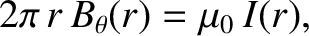
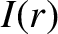 is the current that passes through an Ampèrian loop of radius
is the current that passes through an Ampèrian loop of radius  .
Simple arguments involving proportion reveal that
.
Simple arguments involving proportion reveal that
![\begin{displaymath}I(r) = \left\{
\begin{array}{lcl}
0&\mbox{\hspace{1cm}}&r<a\\...
...2)\right] I&&a\leq r\leq b\\ [0.5ex]
I&&b<r
\end{array}\right..\end{displaymath}](img1658.png)