Next: Ampère's Circuital Law Up: Magnetostatic Fields Previous: Magnetic Vector Potential
 , bounded by a surface
, bounded by a surface  , making use of the divergence theorem (see Section A.20),
then we obtain
, making use of the divergence theorem (see Section A.20),
then we obtain
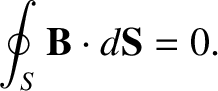 |
(2.264) |
What about magnetic fields generated by permanent magnets (the modern equivalent of loadstones)? Do they also never begin or end? We know that a conventional bar magnet has both a north and south magnetic pole (like the Earth). If we track the magnetic field-lines with a small compass then they all emanate from the north pole, spread out, and eventually re-converge on the south pole. See Figure 2.21. It appears likely (but we cannot prove it with a compass) that the field-lines inside the magnet connect from the south to the north pole so as to form closed loops that never begin or end.
Can we produce an isolated north or south magnetic pole; for instance, by snapping
a bar magnet in two? A compass needle would always point toward an isolated
south pole, so this would act like a negative magnetic charge.
Likewise, a compass needle would always point away from an isolated north
pole, so this would act like a positive magnetic charge.
It is clear, from Figure 2.22,
that if we take a closed surface  containing an isolated
magnetic pole, which is usually termed a magnetic monopole, then
containing an isolated
magnetic pole, which is usually termed a magnetic monopole, then
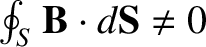 . In fact, the flux will be positive for an isolated
north pole, and negative for an isolated south pole.
It follows from the divergence theorem (see Section A.20) that if
. In fact, the flux will be positive for an isolated
north pole, and negative for an isolated south pole.
It follows from the divergence theorem (see Section A.20) that if
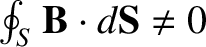 then
then
 . Thus, the statement that
. Thus, the statement that
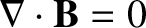 is equivalent to the statement that magnetic monopoles do not exist. It is actually quite possible to formulate electromagnetism so as to
allow for magnetic monopoles. However, as far as we are aware, there are no magnetic
monopoles in the universe.
We know that if we try to make a magnetic monopole by snapping a bar magnet in two
then we just end up with two smaller bar magnets. If we snap one of these smaller
magnets in two then we end up with two even smaller bar magnets. We can continue
this process down to the atomic level without ever producing a magnetic monopole.
In fact, permanent magnetism
is generated by electric currents circulating on the atomic
scale, and so this type of
magnetism is not fundamentally different to the magnetism generated
by macroscopic currents.
is equivalent to the statement that magnetic monopoles do not exist. It is actually quite possible to formulate electromagnetism so as to
allow for magnetic monopoles. However, as far as we are aware, there are no magnetic
monopoles in the universe.
We know that if we try to make a magnetic monopole by snapping a bar magnet in two
then we just end up with two smaller bar magnets. If we snap one of these smaller
magnets in two then we end up with two even smaller bar magnets. We can continue
this process down to the atomic level without ever producing a magnetic monopole.
In fact, permanent magnetism
is generated by electric currents circulating on the atomic
scale, and so this type of
magnetism is not fundamentally different to the magnetism generated
by macroscopic currents.
In conclusion, all steady magnetic fields in the universe are generated by circulating electric currents of some description. Such fields are solenoidal; that is, they have field-lines that never begin or end, and also satisfy the field equation
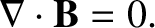 |
(2.265) |
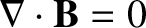 for
steady magnetic fields, but, in fact, it turns out that this is also the case for time-dependent fields.
for
steady magnetic fields, but, in fact, it turns out that this is also the case for time-dependent fields.