We saw in Equation (2.16) that
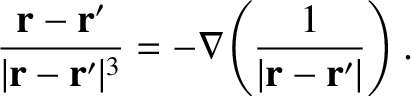 |
(2.249) |
This equation can be combined with the generalized Biot-Savart law, (2.248), to give
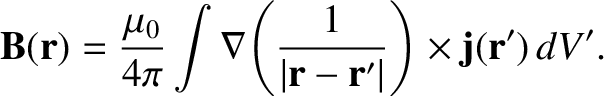 |
(2.250) |
It follows that
 |
(2.251) |
where
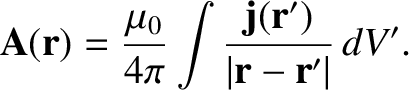 |
(2.252) |
(See Section A.24.)
Here, the vector field
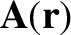 is known as the magnetic vector potential.
is known as the magnetic vector potential.
It is possible to prove that the
magnetic vector potential defined in the previous equation is a divergence-free field.
Note that
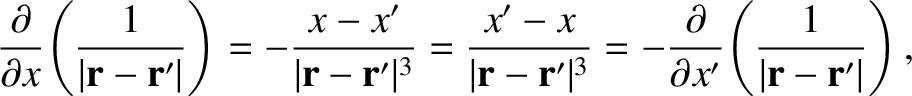 |
(2.253) |
which implies that
 |
(2.254) |
where  is the operator
is the operator
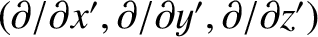 . (See Section A.19.) Taking the divergence of Equation (2.252), and making use of
the previous relation, we obtain
. (See Section A.19.) Taking the divergence of Equation (2.252), and making use of
the previous relation, we obtain
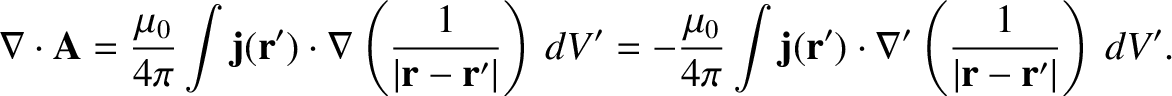 |
(2.255) |
Now,
 |
(2.256) |
However, if
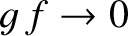 as
as
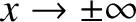 then we can neglect the
first term on the right-hand side of the previous equation, and write
then we can neglect the
first term on the right-hand side of the previous equation, and write
 |
(2.257) |
A simple generalization of this result yields
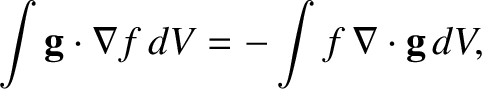 |
(2.258) |
provided that
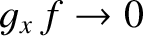 as
as
 , etc cetera.
Thus, Equation (2.255)
yields
, etc cetera.
Thus, Equation (2.255)
yields
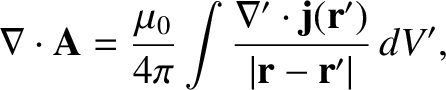 |
(2.259) |
provided that
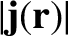 is bounded as
is bounded as
 . Now, the flux of electric charge out of a surface
. Now, the flux of electric charge out of a surface  , enclosing a volume
, enclosing a volume  , is
, is
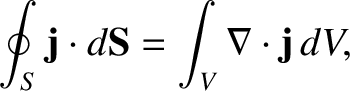 |
(2.260) |
where use has been made of the divergence theorem. (See Section A.20.)
However, for a steady current distribution, this flux must be zero, otherwise positive or negative electric
charge would build up inside  . Moreover, the flux must be zero for all possible volumes,
. Moreover, the flux must be zero for all possible volumes,  , which implies that
, which implies that
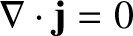 |
(2.261) |
for a steady current distribution. Hence, we deduce from Equation (2.259) that
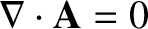 |
(2.262) |
for a steady current distribution.
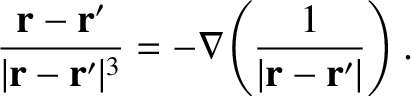
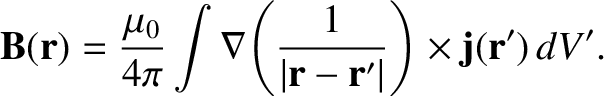
 is known as the magnetic vector potential.
is known as the magnetic vector potential.
 is the operator
is the operator
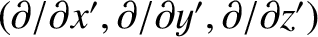 . (See Section A.19.) Taking the divergence of Equation (2.252), and making use of
the previous relation, we obtain
Now,
. (See Section A.19.) Taking the divergence of Equation (2.252), and making use of
the previous relation, we obtain
Now,
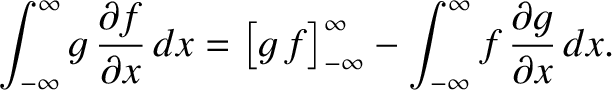
 as
as
 then we can neglect the
first term on the right-hand side of the previous equation, and write
then we can neglect the
first term on the right-hand side of the previous equation, and write

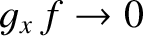 as
as
 , etc cetera.
Thus, Equation (2.255)
yields
provided that
, etc cetera.
Thus, Equation (2.255)
yields
provided that
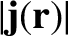 is bounded as
is bounded as
 . Now, the flux of electric charge out of a surface
. Now, the flux of electric charge out of a surface  , enclosing a volume
, enclosing a volume  , is
, is
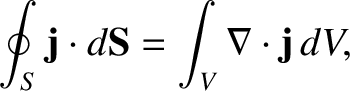
 . Moreover, the flux must be zero for all possible volumes,
. Moreover, the flux must be zero for all possible volumes,  , which implies that
for a steady current distribution. Hence, we deduce from Equation (2.259) that
for a steady current distribution.
, which implies that
for a steady current distribution. Hence, we deduce from Equation (2.259) that
for a steady current distribution.