Next: Quantum Mechanics Up: Relativity and Electromagnetism Previous: Transformation of Electromagnetic Fields
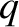 , that is at rest at the origin of an inertial reference frame
, that is at rest at the origin of an inertial reference frame 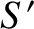 . The electric
and magnetic fields generated by the charge at displacement
. The electric
and magnetic fields generated by the charge at displacement 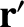 in frame
in frame 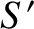 are
are
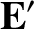 |
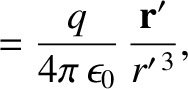 |
(3.286) |
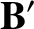 |
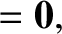 |
(3.287) |
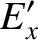 |
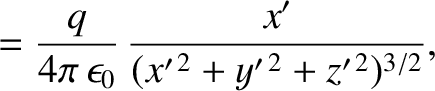 |
(3.288) |
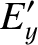 |
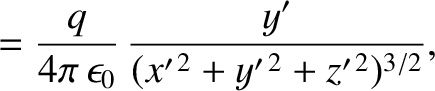 |
(3.289) |
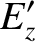 |
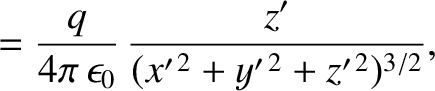 |
(3.290) |
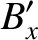 |
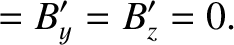 |
(3.291) |
Let us transform to an inertial reference frame, 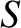 , that is in a standard configuration, and moves with
velocity
, that is in a standard configuration, and moves with
velocity
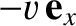 , with respect to frame
, with respect to frame 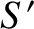 . Thus, in frame
. Thus, in frame 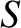 , the charge appears to move with
velocity
, the charge appears to move with
velocity
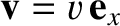 . Making use of the field transformation relations, (3.278)–(3.283),
with primed and unprimed fields swapped, and
. Making use of the field transformation relations, (3.278)–(3.283),
with primed and unprimed fields swapped, and
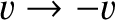 , we obtain
, we obtain
Consider the electric and magnetic fields generated by the charge at some point 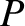 in frame
in frame 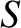 whose displacement is
whose displacement is
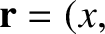
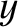 ,
, 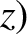 . See Figure 3.18. The displacement of the charge in frame
. See Figure 3.18. The displacement of the charge in frame 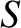 is
is
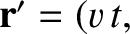 0, 0). Let
0, 0). Let
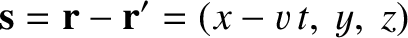 |
(3.298) |
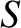 to point
to point 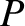 . A Lorentz transformation (see Section 3.2.7) between frames
. A Lorentz transformation (see Section 3.2.7) between frames 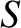 and
and 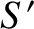 reveals that
reveals that
Let us write
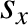 |
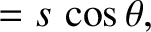 |
(3.302) |
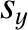 |
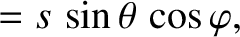 |
(3.303) |
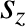 |
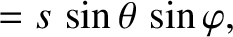 |
(3.304) |
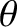 is the angle subtended between
is the angle subtended between 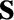 and
and 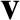 , and
, and 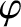 is an
azimuthal angle. See Figure 3.18. It is easily demonstrated from the previous six equations that
is an
azimuthal angle. See Figure 3.18. It is easily demonstrated from the previous six equations that
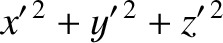 |
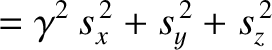 |
|
![$\displaystyle = \left(\gamma^2\,\cos^2\theta + \sin^2\theta\right)s^2=\left[(\gamma^2-1)\,\cos^2\theta+1\right]s^2$](img2861.png) |
||
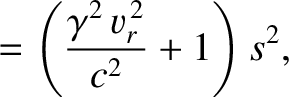 |
(3.305) |
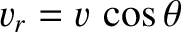 is the component of
is the component of 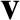 that is directed from the instantaneous position of the charge to the point
that is directed from the instantaneous position of the charge to the point 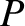 .
Thus, making use of Equations (3.292)–(3.297) and Equations (3.299)–(3.301), we obtain
.
Thus, making use of Equations (3.292)–(3.297) and Equations (3.299)–(3.301), we obtain
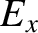 |
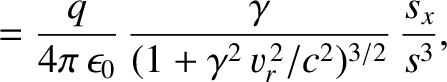 |
(3.306) |
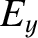 |
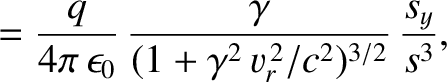 |
(3.307) |
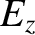 |
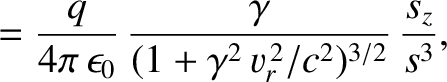 |
(3.308) |
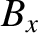 |
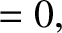 |
(3.309) |
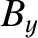 |
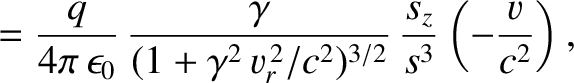 |
(3.310) |
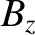 |
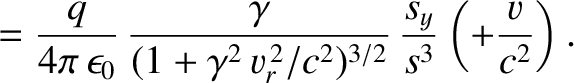 |
(3.311) |
Note that the electric field-lines generated by a moving electric charge are straight-lines that are directed from the
instantaneous position of the charge to the point of observation. At low velocities (i.e., 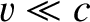 ), the field-lines are
equally spaced around the charge. However, as
), the field-lines are
equally spaced around the charge. However, as
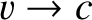 , the field-lines become increasingly bunched in the plane
transverse to the charge's direction of motion that passes through the charge. This is illustrated schematically in Figure 3.19. The magnetic field generated by a moving charge is
, the field-lines become increasingly bunched in the plane
transverse to the charge's direction of motion that passes through the charge. This is illustrated schematically in Figure 3.19. The magnetic field generated by a moving charge is
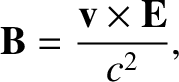 |
(3.312) |
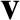 is the charge's velocity, and
is the charge's velocity, and 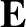 is the electric field generated by the charge.
is the electric field generated by the charge.