Next: Electric Field Up: Electrostatic Fields Previous: Electricity
Consider a system consisting of two point electric charges. Let charge 1 have electric charge 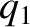 and
displacement
and
displacement 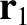 . Let charge 2 have electric charge
. Let charge 2 have electric charge  and displacement
and displacement 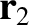 .
Coulomb's law states that the
electrical force exerted on charge
.
Coulomb's law states that the
electrical force exerted on charge 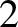 by charge
by charge  is
is
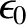 is called the electrical permittivity of free space, and takes the value
is called the electrical permittivity of free space, and takes the value
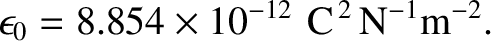 |
(2.3) |
As we saw in Section 1.8.1, according to Newtonian gravity, if two point mass objects of masses 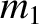 and
and 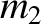 are located at displacements
are located at displacements
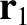 and
and 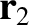 , respectively, then the gravitational force acting on the second object is
, respectively, then the gravitational force acting on the second object is
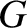 takes the value
takes the value
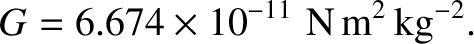 |
(2.5) |
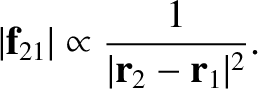 |
(2.6) |
 |
(2.7) |
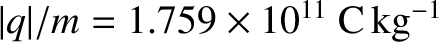 ,
so
,
so
 |
(2.8) |
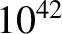 . It would seem a plausible approximation (to say the least) to
start the investigation by neglecting the weaker force altogether. Applying this reasoning to the motion of
particles in the universe, we would expect the universe to be governed entirely by
electrical forces. However, this is not the case. The force that
holds us to the surface of the Earth, and prevents us from
floating off into space, is gravity. The force that causes the Earth
to orbit the Sun is also gravity. In fact, on astronomical lengthscales, gravity is
the dominant force, and electrical forces are largely irrelevant.
The key to understanding this paradox is that there are both
positive and negative electric charges, whereas there are only positive
gravitational “charges.” This implies that gravitational forces are always
cumulative,
whereas electrical forces can cancel one another out. Suppose, for the
sake of argument, that the universe
starts out with randomly distributed
electric charges. Initially, we expect
electrical forces to completely dominate gravitational forces. These forces act to cause
every positive electric
charge to get as far away as possible from the other positive charges in the universe, and as close
as possible to the other negative charges. After a while, we would expect
the positive and
negative electric charges to form close pairs. Just how close is determined by quantum
mechanics, but, in general, it is fairly close; that is, about
. It would seem a plausible approximation (to say the least) to
start the investigation by neglecting the weaker force altogether. Applying this reasoning to the motion of
particles in the universe, we would expect the universe to be governed entirely by
electrical forces. However, this is not the case. The force that
holds us to the surface of the Earth, and prevents us from
floating off into space, is gravity. The force that causes the Earth
to orbit the Sun is also gravity. In fact, on astronomical lengthscales, gravity is
the dominant force, and electrical forces are largely irrelevant.
The key to understanding this paradox is that there are both
positive and negative electric charges, whereas there are only positive
gravitational “charges.” This implies that gravitational forces are always
cumulative,
whereas electrical forces can cancel one another out. Suppose, for the
sake of argument, that the universe
starts out with randomly distributed
electric charges. Initially, we expect
electrical forces to completely dominate gravitational forces. These forces act to cause
every positive electric
charge to get as far away as possible from the other positive charges in the universe, and as close
as possible to the other negative charges. After a while, we would expect
the positive and
negative electric charges to form close pairs. Just how close is determined by quantum
mechanics, but, in general, it is fairly close; that is, about 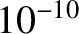 m.
The electrical forces due to the charges in each pair
effectively cancel
one another out on lengthscales much larger than the mutual spacing
of the pair.
However, it is only possible for
gravity to be the dominant long-range force in the universe if the number
of positive electric charges is almost equal to the number of
negative charges. In this
situation, every positive charge can find a negative charge to team up with, and
there are virtually no charges left over. In order for the cancellation
of long-range electrical forces to be effective, the relative difference in the
number of positive and negative electric charges in the universe must be incredibly
small. In fact, positive and negative charges have to cancel one another
to such accuracy that most physicists believe that the net electric
charge of the universe is
exactly zero. But, it is not sufficient for the universe to start out with zero
net charge. Suppose there were some elementary particle process that did not
conserve electric charge. Even if this were to go on at a very low
rate, it would not take long before the fine balance between
positive and negative charges in the universe was wrecked. Thus,
it is important that electric
charge is a conserved quantity (i.e., the net charge of the universe can neither
increase or decrease). As far as we know, this is the case. To date, no
elementary particle reaction has been discovered that can create or destroy net
electric charge.
m.
The electrical forces due to the charges in each pair
effectively cancel
one another out on lengthscales much larger than the mutual spacing
of the pair.
However, it is only possible for
gravity to be the dominant long-range force in the universe if the number
of positive electric charges is almost equal to the number of
negative charges. In this
situation, every positive charge can find a negative charge to team up with, and
there are virtually no charges left over. In order for the cancellation
of long-range electrical forces to be effective, the relative difference in the
number of positive and negative electric charges in the universe must be incredibly
small. In fact, positive and negative charges have to cancel one another
to such accuracy that most physicists believe that the net electric
charge of the universe is
exactly zero. But, it is not sufficient for the universe to start out with zero
net charge. Suppose there were some elementary particle process that did not
conserve electric charge. Even if this were to go on at a very low
rate, it would not take long before the fine balance between
positive and negative charges in the universe was wrecked. Thus,
it is important that electric
charge is a conserved quantity (i.e., the net charge of the universe can neither
increase or decrease). As far as we know, this is the case. To date, no
elementary particle reaction has been discovered that can create or destroy net
electric charge.
In summary, there are two long-range forces in the universe, electricity and gravity. The former is enormously stronger than the latter, but is usually hidden away inside neutral atoms. The fine balance of forces due to negative and positive electric charges starts to break down on atomic scales. In fact, interatomic and intermolecular forces are all electrical in nature. So, electrical forces are basically what prevent us from falling though the floor. But, this is electromagnetism on the microscopic, or atomic, scale. Classical electromagnetism generally describes phenomena in which some sort of violence is done to matter, so that the close pairing of negative and positive electric charges is disrupted, allowing electrical forces to manifest themselves on macroscopic lengthscales. Of course, very little disruption is necessary before gigantic forces are generated. Hence, it is no coincidence that the vast majority of useful machines that humankind has devised during the last century or so are electrical in nature.