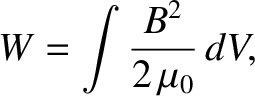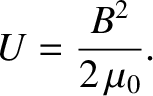Suppose that, at  , a solenoid of inductance
, a solenoid of inductance 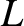 , and resistance
, and resistance  , is connected
across the terminals of a battery of voltage
, is connected
across the terminals of a battery of voltage  . The circuit equation is
. The circuit equation is
 |
(2.358) |
[See Equation (2.326).]
The power output of the battery is 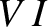 . [Every charge
. [Every charge  that goes around the circuit
falls through a potential difference
that goes around the circuit
falls through a potential difference 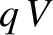 . In order to raise it back to
the starting potential, so that it can perform another circuit, the battery must do
work
. In order to raise it back to
the starting potential, so that it can perform another circuit, the battery must do
work 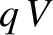 . See Section 2.1.5. The work done per unit time (i.e., the power) is
. See Section 2.1.5. The work done per unit time (i.e., the power) is  , where
, where  is
the number of charges per unit time passing a given point on the circuit.
But,
is
the number of charges per unit time passing a given point on the circuit.
But, 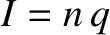 , so the power output is
, so the power output is 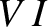 .] Thus, the net work done by the battery in
raising the current in the circuit from zero at time
.] Thus, the net work done by the battery in
raising the current in the circuit from zero at time  to
to 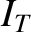 at
time
at
time 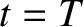 is
is
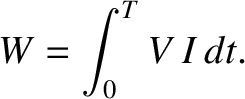 |
(2.359) |
Using the circuit equation (2.358), we obtain
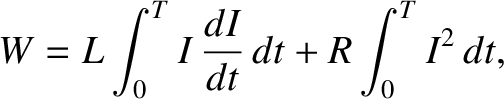 |
(2.360) |
giving
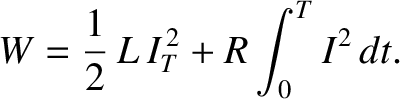 |
(2.361) |
The second term on the right-hand side of the previous equation represents the irreversible conversion of
electrical energy into heat energy by the resistor. (See Section 2.1.11.) The first term is the amount of
energy stored in the solenoid at time  . This energy can be recovered after the
solenoid is disconnected from the battery. Suppose that the battery is disconnected
at time
. This energy can be recovered after the
solenoid is disconnected from the battery. Suppose that the battery is disconnected
at time  . The circuit equation is now
. The circuit equation is now
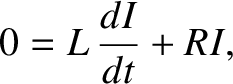 |
(2.362) |
giving
![$\displaystyle I= I_T \exp \left[ - \frac{R}{L} \,(t-T)\right],$](img1834.png) |
(2.363) |
where we have made use of the initial condition
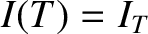 .
Thus, the current
decays away exponentially. The energy stored in the solenoid is dissipated as
heat in the resistor. The total heat energy appearing in the resistor after the
battery is disconnected is
.
Thus, the current
decays away exponentially. The energy stored in the solenoid is dissipated as
heat in the resistor. The total heat energy appearing in the resistor after the
battery is disconnected is
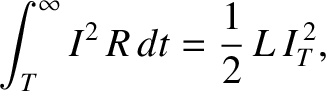 |
(2.364) |
where use has been made of Equation (2.363).
Thus, the heat energy appearing in the resistor is equal to the
energy stored in the solenoid. This energy is actually stored in the magnetic
field generated inside the solenoid.
Consider, again, our circuit with two solenoids wound on top of one another. (See the previous section.) Suppose that
each solenoid is connected to its own battery. The circuit equations are thus
where 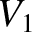 is the voltage of the battery in the first circuit, et cetera. The net work done by the two batteries in increasing the currents in the two circuits,
from zero at time 0, to
is the voltage of the battery in the first circuit, et cetera. The net work done by the two batteries in increasing the currents in the two circuits,
from zero at time 0, to 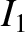 and
and 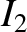 at time
at time  , respectively, is
Thus,
, respectively, is
Thus,
 |
(2.368) |
Clearly, the total magnetic energy stored in the two solenoids is
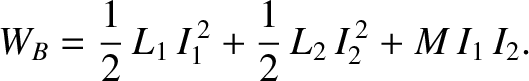 |
(2.369) |
Note that the mutual inductance term increases the stored magnetic energy if 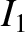 and
and
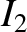 are of the same sign; that is, if the currents in the two solenoids flow
in the same direction, so that they generate magnetic fields that reinforce
one another. Conversely, the mutual inductance term decreases the stored
magnetic energy if
are of the same sign; that is, if the currents in the two solenoids flow
in the same direction, so that they generate magnetic fields that reinforce
one another. Conversely, the mutual inductance term decreases the stored
magnetic energy if 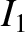 and
and 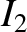 are of the opposite sign. However, the total
stored energy can never be negative, otherwise the coils
would constitute a power source (a negative stored energy is equivalent to
a positive generated energy). Thus,
are of the opposite sign. However, the total
stored energy can never be negative, otherwise the coils
would constitute a power source (a negative stored energy is equivalent to
a positive generated energy). Thus,
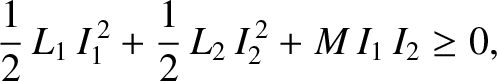 |
(2.370) |
which can be written
 |
(2.371) |
assuming that
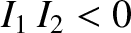 . It follows that
. It follows that
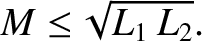 |
(2.372) |
The equality sign corresponds to the situation in which
all of the magnetic flux generated by one solenoid passes through the other. If some of
the flux misses then the inequality sign is appropriate.
In fact, the previous formula is valid
for any two inductively coupled circuits, and effectively sets an upper limit
on their mutual inductance.
We intimated previously that the energy stored in an solenoid is actually
stored in the surrounding magnetic field. Let us now obtain an
explicit formula for the energy stored in a magnetic field. Consider an ideal
cylindrical solenoid. The energy stored in the solenoid when a current  flows through it
is
flows through it
is
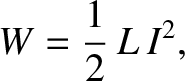 |
(2.373) |
where 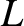 is the self inductance. We know that
is the self inductance. We know that
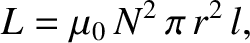 |
(2.374) |
where  is the number of turns per unit length of the
solenoid,
is the number of turns per unit length of the
solenoid,  the radius, and
the radius, and  the length. [See Equation (2.324).] The magnetic field inside the solenoid is approximately
uniform, with magnitude
the length. [See Equation (2.324).] The magnetic field inside the solenoid is approximately
uniform, with magnitude
 |
(2.375) |
and is approximately zero outside the solenoid. [See Equation (2.279).] Equation (2.373) can be rewritten
 |
(2.376) |
where
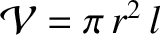 is the volume of the solenoid. The previous formula strongly
suggests that a magnetic field possesses an energy density
is the volume of the solenoid. The previous formula strongly
suggests that a magnetic field possesses an energy density
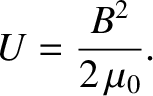 |
(2.377) |
Let us now examine a more general proof of the previous formula. Consider a system
of  circuits (labeled
circuits (labeled 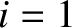 to
to  ), each carrying a current
), each carrying a current 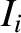 .
The magnetic flux through the
.
The magnetic flux through the  th circuit is written [see Equation (2.315)]
th circuit is written [see Equation (2.315)]
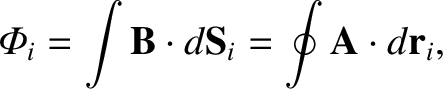 |
(2.378) |
where
 , and
, and
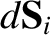 and
and
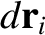 denote a
surface element and a line element of this circuit, respectively. The
back-emf induced in the
denote a
surface element and a line element of this circuit, respectively. The
back-emf induced in the  th circuit follows from Faraday's law:
th circuit follows from Faraday's law:
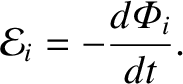 |
(2.379) |
[See Equation (2.284).]
The rate of work of the battery that maintains the current 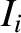 in the
in the  th circuit
against this back-emf is
th circuit
against this back-emf is
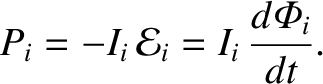 |
(2.380) |
Thus, the total work required
to raise the currents in the  circuits from zero at time
0, to
circuits from zero at time
0, to 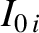 at time
at time  , is
, is
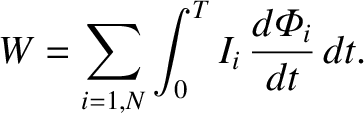 |
(2.381) |
The previous expression for the work done is, of course, equivalent to the total
energy stored in the magnetic field surrounding the various circuits.
This energy is independent of the manner in which the currents
are set up.
Suppose, for the sake of simplicity, that the currents are ramped up linearly,
so that
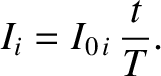 |
(2.382) |
The fluxes are proportional to the currents, so they must also ramp up linearly; that is,
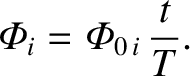 |
(2.383) |
It follows that
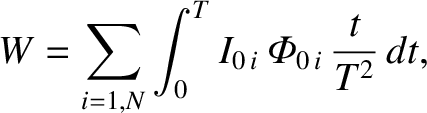 |
(2.384) |
giving
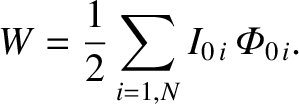 |
(2.385) |
So, if instantaneous currents 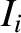 flow in the
flow in the  circuits, which link
instantaneous fluxes
circuits, which link
instantaneous fluxes
 , then the instantaneous stored energy is
, then the instantaneous stored energy is
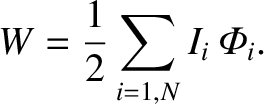 |
(2.386) |
Equations (2.378) and (2.386) imply that
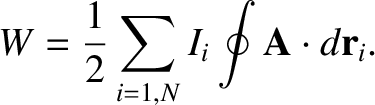 |
(2.387) |
It is convenient, at this stage, to replace our  line currents by
line currents by
 current
distributions of
small, but finite, cross-sectional area.
Equation (2.387)
transforms to give
current
distributions of
small, but finite, cross-sectional area.
Equation (2.387)
transforms to give
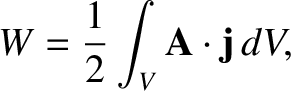 |
(2.388) |
where  is a volume that contains all of the circuits.
Note that for an element of the
is a volume that contains all of the circuits.
Note that for an element of the  th circuit,
th circuit,
 and
and
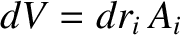 , where
, where 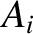 is the cross-sectional area of the
circuit.
Now,
is the cross-sectional area of the
circuit.
Now,
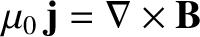 [see Equation (2.271)], so
[see Equation (2.271)], so
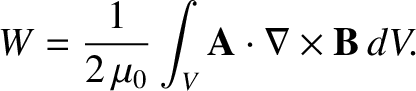 |
(2.389) |
However,
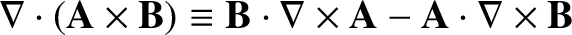 |
(2.390) |
(see Section A.24),
which implies that
![$\displaystyle W = \frac{1}{2\,\mu_0} \int_V \left[- \nabla\cdot ({\bf A} \times{\bf B})
+{\bf B}\cdot \nabla \times {\bf A} \right] \,dV.$](img1880.png) |
(2.391) |
Using the divergence theorem (see Section A.20), and
 , we obtain
, we obtain
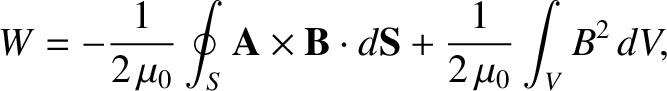 |
(2.392) |
where  is the bounding surface of some volume
is the bounding surface of some volume  . Let us take this surface
to infinity. It is easily demonstrated that the magnetic field generated by a current
loop falls of like
. Let us take this surface
to infinity. It is easily demonstrated that the magnetic field generated by a current
loop falls of like  at large distances. (See Section 2.2.7.) The vector potential
falls off like
at large distances. (See Section 2.2.7.) The vector potential
falls off like  . However, the area of surface
. However, the area of surface  only increases like
only increases like 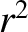 .
It follows that the surface integral is negligible in the limit
.
It follows that the surface integral is negligible in the limit
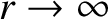 .
Thus, the previous expression reduces to
.
Thus, the previous expression reduces to
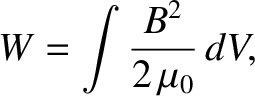 |
(2.393) |
where the integral is over all space.
Because this expression is valid for any magnetic field whatsoever, we can safely conclude
that the energy density of a general magnetic field generated by a system of electrical circuits is given by
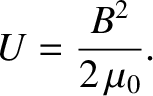 |
(2.394) |
Note, finally, that the fact that a magnetic field possesses an energy density demonstrates that it has a real physical
existence, and is not merely an aid to calculating the forces that current-carrying wires exert on one another.
 , a solenoid of inductance
, a solenoid of inductance  , and resistance
, and resistance  , is connected
across the terminals of a battery of voltage
, is connected
across the terminals of a battery of voltage  . The circuit equation is
[See Equation (2.326).]
The power output of the battery is
. The circuit equation is
[See Equation (2.326).]
The power output of the battery is 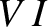 . [Every charge
. [Every charge  that goes around the circuit
falls through a potential difference
that goes around the circuit
falls through a potential difference 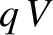 . In order to raise it back to
the starting potential, so that it can perform another circuit, the battery must do
work
. In order to raise it back to
the starting potential, so that it can perform another circuit, the battery must do
work 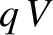 . See Section 2.1.5. The work done per unit time (i.e., the power) is
. See Section 2.1.5. The work done per unit time (i.e., the power) is  , where
, where  is
the number of charges per unit time passing a given point on the circuit.
But,
is
the number of charges per unit time passing a given point on the circuit.
But, 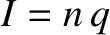 , so the power output is
, so the power output is 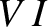 .] Thus, the net work done by the battery in
raising the current in the circuit from zero at time
.] Thus, the net work done by the battery in
raising the current in the circuit from zero at time  to
to 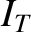 at
time
at
time 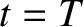 is
is
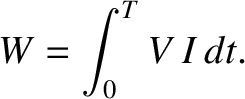
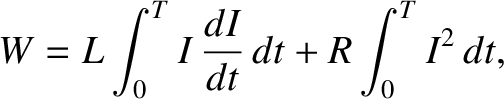
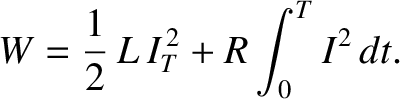
 . This energy can be recovered after the
solenoid is disconnected from the battery. Suppose that the battery is disconnected
at time
. This energy can be recovered after the
solenoid is disconnected from the battery. Suppose that the battery is disconnected
at time  . The circuit equation is now
. The circuit equation is now
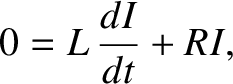
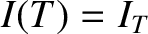 .
Thus, the current
decays away exponentially. The energy stored in the solenoid is dissipated as
heat in the resistor. The total heat energy appearing in the resistor after the
battery is disconnected is
.
Thus, the current
decays away exponentially. The energy stored in the solenoid is dissipated as
heat in the resistor. The total heat energy appearing in the resistor after the
battery is disconnected is
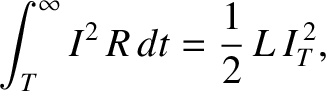
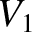
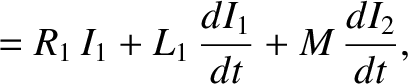
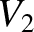
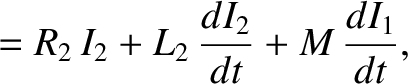
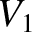 is the voltage of the battery in the first circuit, et cetera. The net work done by the two batteries in increasing the currents in the two circuits,
from zero at time 0, to
is the voltage of the battery in the first circuit, et cetera. The net work done by the two batteries in increasing the currents in the two circuits,
from zero at time 0, to 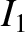 and
and 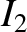 at time
at time  , respectively, is
, respectively, is
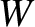

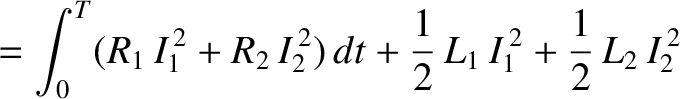
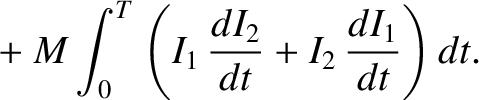

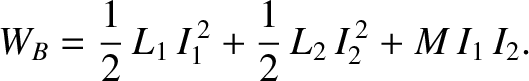
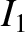 and
and
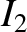 are of the same sign; that is, if the currents in the two solenoids flow
in the same direction, so that they generate magnetic fields that reinforce
one another. Conversely, the mutual inductance term decreases the stored
magnetic energy if
are of the same sign; that is, if the currents in the two solenoids flow
in the same direction, so that they generate magnetic fields that reinforce
one another. Conversely, the mutual inductance term decreases the stored
magnetic energy if 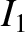 and
and 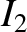 are of the opposite sign. However, the total
stored energy can never be negative, otherwise the coils
would constitute a power source (a negative stored energy is equivalent to
a positive generated energy). Thus,
are of the opposite sign. However, the total
stored energy can never be negative, otherwise the coils
would constitute a power source (a negative stored energy is equivalent to
a positive generated energy). Thus,
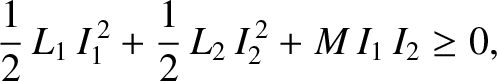

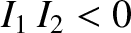 . It follows that
. It follows that
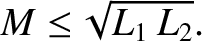
 flows through it
is
flows through it
is
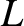 is the self inductance. We know that
is the self inductance. We know that
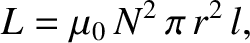
 is the number of turns per unit length of the
solenoid,
is the number of turns per unit length of the
solenoid,  the radius, and
the radius, and  the length. [See Equation (2.324).] The magnetic field inside the solenoid is approximately
uniform, with magnitude
the length. [See Equation (2.324).] The magnetic field inside the solenoid is approximately
uniform, with magnitude


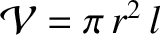 is the volume of the solenoid. The previous formula strongly
suggests that a magnetic field possesses an energy density
is the volume of the solenoid. The previous formula strongly
suggests that a magnetic field possesses an energy density
 circuits (labeled
circuits (labeled  to
to  ), each carrying a current
), each carrying a current 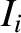 .
The magnetic flux through the
.
The magnetic flux through the  th circuit is written [see Equation (2.315)]
th circuit is written [see Equation (2.315)]
 , and
, and
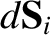 and
and
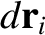 denote a
surface element and a line element of this circuit, respectively. The
back-emf induced in the
denote a
surface element and a line element of this circuit, respectively. The
back-emf induced in the  th circuit follows from Faraday's law:
th circuit follows from Faraday's law:
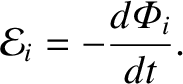
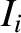 in the
in the  th circuit
against this back-emf is
th circuit
against this back-emf is
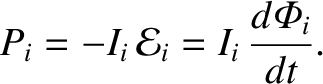
 circuits from zero at time
0, to
circuits from zero at time
0, to 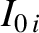 at time
at time  , is
, is
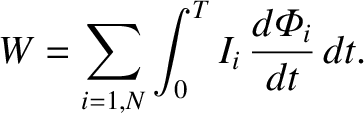
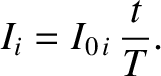
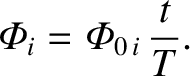
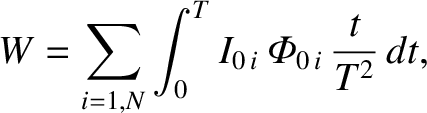
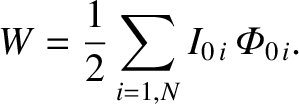
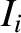 flow in the
flow in the  circuits, which link
instantaneous fluxes
circuits, which link
instantaneous fluxes
 , then the instantaneous stored energy is
, then the instantaneous stored energy is
 line currents by
line currents by
 current
distributions of
small, but finite, cross-sectional area.
Equation (2.387)
transforms to give
current
distributions of
small, but finite, cross-sectional area.
Equation (2.387)
transforms to give
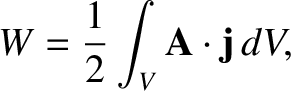
 is a volume that contains all of the circuits.
Note that for an element of the
is a volume that contains all of the circuits.
Note that for an element of the  th circuit,
th circuit,
 and
and
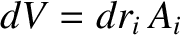 , where
, where 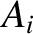 is the cross-sectional area of the
circuit.
Now,
is the cross-sectional area of the
circuit.
Now,
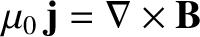 [see Equation (2.271)], so
[see Equation (2.271)], so
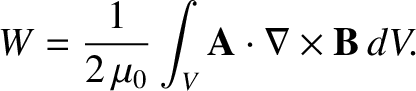
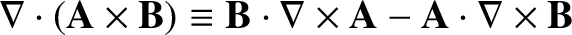
![$\displaystyle W = \frac{1}{2\,\mu_0} \int_V \left[- \nabla\cdot ({\bf A} \times{\bf B})
+{\bf B}\cdot \nabla \times {\bf A} \right] \,dV.$](img1880.png)
 , we obtain
, we obtain
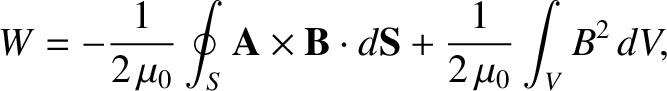
 is the bounding surface of some volume
is the bounding surface of some volume  . Let us take this surface
to infinity. It is easily demonstrated that the magnetic field generated by a current
loop falls of like
. Let us take this surface
to infinity. It is easily demonstrated that the magnetic field generated by a current
loop falls of like  at large distances. (See Section 2.2.7.) The vector potential
falls off like
at large distances. (See Section 2.2.7.) The vector potential
falls off like  . However, the area of surface
. However, the area of surface  only increases like
only increases like 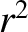 .
It follows that the surface integral is negligible in the limit
.
It follows that the surface integral is negligible in the limit
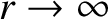 .
Thus, the previous expression reduces to
.
Thus, the previous expression reduces to