Next: Alternating Current Generators Up: Magnetic Induction Previous: Magnetic Energy
 slides along a
U-shaped conducting frame in the presence of a uniform magnetic field.
This circuit is illustrated in Figure 2.31. Suppose, for the sake of simplicity, that the
magnetic field is directed perpendicular to the plane of the circuit. To be
more exact, the magnetic field is directed into the page in the figure.
Suppose, further, that the rod moves to the right at the constant speed
slides along a
U-shaped conducting frame in the presence of a uniform magnetic field.
This circuit is illustrated in Figure 2.31. Suppose, for the sake of simplicity, that the
magnetic field is directed perpendicular to the plane of the circuit. To be
more exact, the magnetic field is directed into the page in the figure.
Suppose, further, that the rod moves to the right at the constant speed
 .
.
The magnetic flux passing through the circuit is simply the product of
the perpendicular magnetic field-strength,  , and the area of the circuit,
, and the area of the circuit,
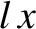 , where
, where  determines the position of the sliding rod.
Thus,
determines the position of the sliding rod.
Thus,
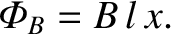 |
(2.395) |
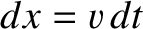 in a
time interval
in a
time interval 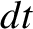 , so in the same time interval the magnetic
flux passing through the circuit increases by
, so in the same time interval the magnetic
flux passing through the circuit increases by
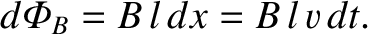 |
(2.396) |
 generated around the circuit is given by
Thus, the emf generated in the circuit by the moving rod is simply the product of
the magnetic field-strength, the length of the rod, and the velocity of
the rod.
If the magnetic field is not perpendicular to the circuit,
but instead subtends an angle
generated around the circuit is given by
Thus, the emf generated in the circuit by the moving rod is simply the product of
the magnetic field-strength, the length of the rod, and the velocity of
the rod.
If the magnetic field is not perpendicular to the circuit,
but instead subtends an angle  with respect to the normal direction
to the plane of the circuit, then it is easily demonstrated that the so-called
motional emf generated in the circuit by the moving rod is
with respect to the normal direction
to the plane of the circuit, then it is easily demonstrated that the so-called
motional emf generated in the circuit by the moving rod is
 |
(2.398) |
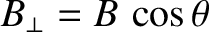 is the component of the magnetic field
that is perpendicular to the plane of the circuit.
is the component of the magnetic field
that is perpendicular to the plane of the circuit.
Because the magnetic flux linking the circuit increases in time, by Lenz's law, the
emf acts in the negative direction (i.e., in the opposite sense to the
fingers of a right-hand, if the thumb points along the
direction of the magnetic field). The emf,  , therefore, acts in a
counter-clockwise direction in the figure. If
, therefore, acts in a
counter-clockwise direction in the figure. If  is the total resistance of the circuit
then this emf drives an counter-clockwise electric current of magnitude
is the total resistance of the circuit
then this emf drives an counter-clockwise electric current of magnitude
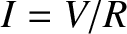 around the circuit. Of course, this current generates a magnetic field that acts to
reduce the increase in the magnetic flux passing through the circuit.
around the circuit. Of course, this current generates a magnetic field that acts to
reduce the increase in the magnetic flux passing through the circuit.
But, where does the motional emf come from? Let us again remind ourselves what an
we mean by an emf. When we say that an emf  acts around the circuit
in the counter-clockwise direction, what we really mean is that a charge
acts around the circuit
in the counter-clockwise direction, what we really mean is that a charge  that circulates once around the circuit in a counter-clockwise direction
acquires the energy
that circulates once around the circuit in a counter-clockwise direction
acquires the energy 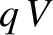 . The only manner in which the charge
can acquire this energy is if something does work
on it as it circulates.
Let us assume that the charge circulates very slowly. The magnetic
field exerts a negligibly small force on the charge when it is traversing the
non-moving part of the circuit (because the charge is moving very slowly).
However, when the charge is traversing the moving rod
it experiences an upward (in the figure) magnetic force of magnitude
. The only manner in which the charge
can acquire this energy is if something does work
on it as it circulates.
Let us assume that the charge circulates very slowly. The magnetic
field exerts a negligibly small force on the charge when it is traversing the
non-moving part of the circuit (because the charge is moving very slowly).
However, when the charge is traversing the moving rod
it experiences an upward (in the figure) magnetic force of magnitude 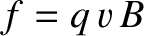 (assuming that
(assuming that
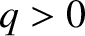 ). (See Section 2.2.4.) The net work done on the charge by this force as
it traverses the rod is
). (See Section 2.2.4.) The net work done on the charge by this force as
it traverses the rod is
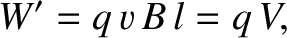 |
(2.399) |
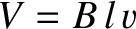 . Thus, it would appear that the motional emf
generated around the circuit can be accounted for in terms of the
magnetic force exerted
on charges traversing the moving rod.
. Thus, it would appear that the motional emf
generated around the circuit can be accounted for in terms of the
magnetic force exerted
on charges traversing the moving rod.
However, there is something
seriously wrong with the previous explanation.
We seem to be saying that the charge acquires the energy 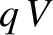 from the magnetic field as it moves around the circuit once in a
counter-clockwise direction. But, this is impossible, because a magnetic field
cannot do work on an electric charge. (See Section 2.2.4.)
from the magnetic field as it moves around the circuit once in a
counter-clockwise direction. But, this is impossible, because a magnetic field
cannot do work on an electric charge. (See Section 2.2.4.)
Let us look at the problem from the point of view of a charge
 traversing the moving rod. In the frame of reference of the rod,
the charge only moves very slowly, so the magnetic force acting on it is negligible. In fact, only an electric field can exert a significant
force on a slowly moving charge. In order to account for the motional emf generated
around the circuit, we need the charge to experience an upward force of
magnitude
traversing the moving rod. In the frame of reference of the rod,
the charge only moves very slowly, so the magnetic force acting on it is negligible. In fact, only an electric field can exert a significant
force on a slowly moving charge. In order to account for the motional emf generated
around the circuit, we need the charge to experience an upward force of
magnitude  . The only way in which this is possible is if the charge
sees an upward pointing electric field of magnitude
. The only way in which this is possible is if the charge
sees an upward pointing electric field of magnitude
 |
(2.400) |

More generally, if a conductor moves in the laboratory frame
with velocity  in the presence of a magnetic field
in the presence of a magnetic field  then
a charge
then
a charge  inside the conductor experiences a magnetic force
inside the conductor experiences a magnetic force
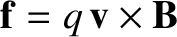 . In the frame of the conductor, in which the charge is
essentially stationary, the same force takes the form of an electric
force
. In the frame of the conductor, in which the charge is
essentially stationary, the same force takes the form of an electric
force
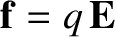 , where
, where  is the electric field in
the frame of reference of the conductor. Thus,
if a conductor moves with velocity
is the electric field in
the frame of reference of the conductor. Thus,
if a conductor moves with velocity  through a magnetic field
through a magnetic field  then the electric field
then the electric field  that appears in the rest frame of the conductor
is given by
that appears in the rest frame of the conductor
is given by