Next: Charged Particle Motion in Up: Magnetostatic Fields Previous: Ampère's Law
Let  be the
(uniform) cross-sectional area of the wire, and let
be the
(uniform) cross-sectional area of the wire, and let  be the number density
of mobile charges in the wire. Suppose that the
mobile charges each have charge
be the number density
of mobile charges in the wire. Suppose that the
mobile charges each have charge  and drift velocity
and drift velocity  .
We must assume that
the wire also contains stationary charges, of charge
.
We must assume that
the wire also contains stationary charges, of charge 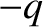 and number density
and number density
 , say, so that the net charge density in the wire is zero. In most conductors, the
mobile charges are electrons, and the stationary charges are ions.
The magnitude of the electric current flowing through the wire is simply the
number of coulombs per second that flow past a given point. In one second,
a mobile charge moves a distance
, say, so that the net charge density in the wire is zero. In most conductors, the
mobile charges are electrons, and the stationary charges are ions.
The magnitude of the electric current flowing through the wire is simply the
number of coulombs per second that flow past a given point. In one second,
a mobile charge moves a distance  , so all of the charges contained in a
cylinder of cross-sectional area
, so all of the charges contained in a
cylinder of cross-sectional area  and length
and length  flow past a given point.
Thus, the magnitude of the current is
flow past a given point.
Thus, the magnitude of the current is
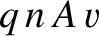 . The direction of the
current is the same as the direction of motion of the charges (i.e.,
. The direction of the
current is the same as the direction of motion of the charges (i.e.,
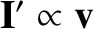 ), so the
vector current is
), so the
vector current is
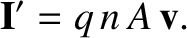 |
(2.209) |
According to Equation (2.205), the force per unit length acting on the wire is
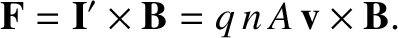 |
(2.210) |
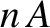 moving charges. So, assuming
that each charge is subject to an equal force from the magnetic field (and we have
no reason to suppose otherwise), the magnetic
force acting on an individual charge is
This formula implies that the magnitude of the magnetic force exerted on a moving
charged particle is the product of the particle's electric charge, its
velocity, the
magnetic field-strength, and the sine of the angle subtended between the
particle's direction of motion and the direction of the magnetic field. (See Section A.8.)
The force is directed perpendicular to both the magnetic field and the
particle's instantaneous direction of motion.
moving charges. So, assuming
that each charge is subject to an equal force from the magnetic field (and we have
no reason to suppose otherwise), the magnetic
force acting on an individual charge is
This formula implies that the magnitude of the magnetic force exerted on a moving
charged particle is the product of the particle's electric charge, its
velocity, the
magnetic field-strength, and the sine of the angle subtended between the
particle's direction of motion and the direction of the magnetic field. (See Section A.8.)
The force is directed perpendicular to both the magnetic field and the
particle's instantaneous direction of motion.
We can combine the previous equation with Equation (2.10) to give the force acting on an electric charge  moving
with velocity
moving
with velocity  in an electric field
in an electric field  and a magnetic field
and a magnetic field
 :
:
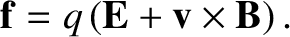 |
(2.212) |
The
equation of motion of a free particle of charge  and
mass
and
mass  moving in electric and
magnetic fields is
moving in electric and
magnetic fields is
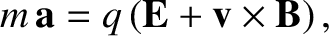 |
(2.213) |
 is the
particle's acceleration.
This equation of motion was verified in a famous experiment carried out
by the Cambridge physicist J.J. Thompson in 1897. Thompson was investigating
cathode rays, a then mysterious form of radiation emitted by a heated
metal element held at a large negative voltage (i.e., a cathode) with respect
to another metal element (i.e., an anode) in an evacuated tube.
German physicists maintained that cathode rays were
a form of electromagnetic radiation, whereas British and French physicists suspected
that they were, in reality, a stream of charged particles. Thompson was able to
demonstrate that the latter view was correct. In Thompson's experiment, the
cathode rays pass though a region of crossed electric and magnetic
fields (still in vacuum). The fields are perpendicular to the original
trajectory of the rays, and are also mutually perpendicular.
is the
particle's acceleration.
This equation of motion was verified in a famous experiment carried out
by the Cambridge physicist J.J. Thompson in 1897. Thompson was investigating
cathode rays, a then mysterious form of radiation emitted by a heated
metal element held at a large negative voltage (i.e., a cathode) with respect
to another metal element (i.e., an anode) in an evacuated tube.
German physicists maintained that cathode rays were
a form of electromagnetic radiation, whereas British and French physicists suspected
that they were, in reality, a stream of charged particles. Thompson was able to
demonstrate that the latter view was correct. In Thompson's experiment, the
cathode rays pass though a region of crossed electric and magnetic
fields (still in vacuum). The fields are perpendicular to the original
trajectory of the rays, and are also mutually perpendicular.
Let us analyze Thompson's experiment. Suppose that
the rays are originally traveling in the  -direction, and are subject to
a uniform electric field
-direction, and are subject to
a uniform electric field  in the
in the  -direction, and a uniform magnetic
field
-direction, and a uniform magnetic
field  in the
in the 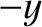 -direction. See Figure 2.16. Let us assume, as Thompson did, that cathode
rays are a stream of particles of mass
-direction. See Figure 2.16. Let us assume, as Thompson did, that cathode
rays are a stream of particles of mass  and charge
and charge  . The
. The
 -component of the equation of motion of an individual particle is
-component of the equation of motion of an individual particle is
 is the
is the  -component of its velocity, and
-component of its velocity, and 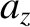 the
the  -component of its acceleration.
Thompson started off his experiment by
only turning on the electric field in his apparatus, and
measuring the
deflection
-component of its acceleration.
Thompson started off his experiment by
only turning on the electric field in his apparatus, and
measuring the
deflection 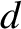 of the rays in the
of the rays in the  -direction after they had traveled a
distance
-direction after they had traveled a
distance  through the field. Now, a particle subject to a
constant acceleration
through the field. Now, a particle subject to a
constant acceleration 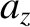 in the
in the  -direction is deflected a
distance
-direction is deflected a
distance
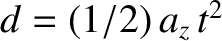 in a time
in a time  .
Thus,
where the time of flight
.
Thus,
where the time of flight  is replaced by
is replaced by 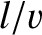 . This replacement is only
valid if
. This replacement is only
valid if 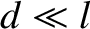 (i.e., if the deflection of
the rays is small compared to the distance that they travel
through the electric field), which is assumed to be the case.
Next, Thompson turned on
the magnetic field in his apparatus, and adjusted it so that the cathode rays were
no longer deflected. The lack of deflection implies that the net force on the
particles in the
(i.e., if the deflection of
the rays is small compared to the distance that they travel
through the electric field), which is assumed to be the case.
Next, Thompson turned on
the magnetic field in his apparatus, and adjusted it so that the cathode rays were
no longer deflected. The lack of deflection implies that the net force on the
particles in the  -direction is zero. In other words, the electric and
magnetic forces balance exactly. It follows from Equation (2.214)
that, with a properly adjusted magnetic field-strength,
Thus, Equations (2.215) and (2.216)
can be combined and rearranged to give the charge to mass ratio of
the particles in terms of measured quantities:
-direction is zero. In other words, the electric and
magnetic forces balance exactly. It follows from Equation (2.214)
that, with a properly adjusted magnetic field-strength,
Thus, Equations (2.215) and (2.216)
can be combined and rearranged to give the charge to mass ratio of
the particles in terms of measured quantities:
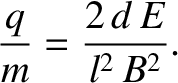 |
(2.217) |
 .
.
A decade later, in 1908, Robert
Millikan performed his famous oil drop experiment in which he
discovered that
mobile electric charges are quantized in units of
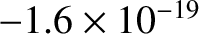 C.
Assuming that mobile electric charges and the particles that
make up cathode rays are one and the same thing,
Thompson's and Millikan's experiments imply that the mass
of these particles is
C.
Assuming that mobile electric charges and the particles that
make up cathode rays are one and the same thing,
Thompson's and Millikan's experiments imply that the mass
of these particles is
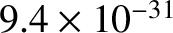 kg. Of course, this is the mass of
an electron (the modern value is
kg. Of course, this is the mass of
an electron (the modern value is
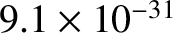 kg), and
kg), and
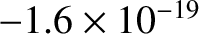 C is the charge of an electron. Thus, cathode rays are, in fact,
streams of electrons that are emitted from a heated cathode, and then
accelerated because of the large voltage difference between the cathode and anode.
C is the charge of an electron. Thus, cathode rays are, in fact,
streams of electrons that are emitted from a heated cathode, and then
accelerated because of the large voltage difference between the cathode and anode.
If a particle is subject to a force 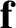 that causes it
to displace by
that causes it
to displace by
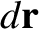 then the work done on the particle by the
force is
then the work done on the particle by the
force is
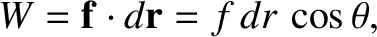 |
(2.218) |
 is the angle subtended between the force and the displacement. (See Section 1.3.2.) However, this angle is always
is the angle subtended between the force and the displacement. (See Section 1.3.2.) However, this angle is always 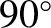 for the force exerted by a magnetic field on
a charged particle, because the magnetic force is
always perpendicular to the particle's instantaneous direction of motion.
It follows that
a magnetic field is unable to do work on a charged particle.
In other words, a
charged particle can never gain or lose energy due to interaction with
a magnetic field. On the other hand, a charged particle can certainly gain
or lose energy due to interaction with an electric field.
Thus, magnetic
fields are often used in particle accelerators to guide charged particle motion (e.g., in a circle), but the
actual acceleration is always performed by electric fields.
for the force exerted by a magnetic field on
a charged particle, because the magnetic force is
always perpendicular to the particle's instantaneous direction of motion.
It follows that
a magnetic field is unable to do work on a charged particle.
In other words, a
charged particle can never gain or lose energy due to interaction with
a magnetic field. On the other hand, a charged particle can certainly gain
or lose energy due to interaction with an electric field.
Thus, magnetic
fields are often used in particle accelerators to guide charged particle motion (e.g., in a circle), but the
actual acceleration is always performed by electric fields.