Next: Hall Effect Up: Magnetostatic Fields Previous: Lorentz Force Law
 moves in a circular orbit of
radius
moves in a circular orbit of
radius 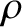 with a constant speed
with a constant speed  . As is well known, the acceleration of the
particle is of magnitude
. As is well known, the acceleration of the
particle is of magnitude 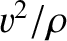 , and is always
directed toward the center of the orbit. It follows that the
acceleration is always perpendicular to the particle's instantaneous
direction of motion.
, and is always
directed toward the center of the orbit. It follows that the
acceleration is always perpendicular to the particle's instantaneous
direction of motion.
We have seen that the force exerted on an electrically charged particle by a magnetic
field is always perpendicular to its instantaneous direction of motion.
Does this imply that the field causes the particle to execute a circular
orbit? Consider the case shown in Figure 2.17. Suppose that a
particle of positive charge  and mass
and mass  moves in a plane perpendicular
to a uniform magnetic field
moves in a plane perpendicular
to a uniform magnetic field  . In the figure, the field is directed into
the plane of the paper. Suppose that the particle moves, in a
counter-clockwise manner, with constant
speed
. In the figure, the field is directed into
the plane of the paper. Suppose that the particle moves, in a
counter-clockwise manner, with constant
speed  (recall that the magnetic field cannot do work on the
particle, so it cannot affect its speed), in a circular orbit of radius
(recall that the magnetic field cannot do work on the
particle, so it cannot affect its speed), in a circular orbit of radius 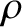 .
The magnetic force acting on the particle is
of magnitude
.
The magnetic force acting on the particle is
of magnitude 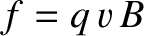 and, according to Equation (2.211), this force is always
directed toward the center of the orbit. Thus, if
and, according to Equation (2.211), this force is always
directed toward the center of the orbit. Thus, if
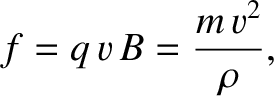 |
(2.219) |
It is clear, from Equation (2.221), that the angular frequency of gyration of a charged
particle in a known magnetic field can be used to determine its charge to
mass ratio,  . Furthermore, if the speed of the particle is known then
the radius of the orbit can also be used to determine
. Furthermore, if the speed of the particle is known then
the radius of the orbit can also be used to determine  , via Equation (2.220).
In the past, this method was used extensively in high energy physics experiments to identify particles from
photographs of the tracks that they left in magnetized cloud chambers or bubble
chambers. It is, of course, easy to differentiate positively charged particles
from negatively charged ones using the direction of deflection of the
particles in the magnetic field.
, via Equation (2.220).
In the past, this method was used extensively in high energy physics experiments to identify particles from
photographs of the tracks that they left in magnetized cloud chambers or bubble
chambers. It is, of course, easy to differentiate positively charged particles
from negatively charged ones using the direction of deflection of the
particles in the magnetic field.
We have seen that a charged particle placed in a magnetic field executes a
circular orbit in the plane perpendicular to the direction of the field.
However, we can also add an arbitrary drift along the direction
of the magnetic field. This follows because the force
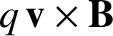 acting on the particle only depends on the component of the particle's velocity
that is perpendicular to the direction of magnetic field (the vector
product of two parallel vectors is always zero because the angle
acting on the particle only depends on the component of the particle's velocity
that is perpendicular to the direction of magnetic field (the vector
product of two parallel vectors is always zero because the angle  they subtend is zero). (See Section A.8.) The combination of circular motion in the
plane perpendicular to the magnetic field, and uniform motion along the
direction of the
field, gives rise to a spiral trajectory of a charged particle in
a magnetic field, where the field forms the axis of the spiral. See Figure 2.18.
they subtend is zero). (See Section A.8.) The combination of circular motion in the
plane perpendicular to the magnetic field, and uniform motion along the
direction of the
field, gives rise to a spiral trajectory of a charged particle in
a magnetic field, where the field forms the axis of the spiral. See Figure 2.18.